
分析 (1)由题意和等差中项的性质列出关系式并化简,分别代入$\frac{{a}_{n+1}-{b}_{n+1}}{{a}_{n}-{b}_{n}}$和$\frac{{a}_{n+1}+2{b}_{n+1}}{{a}_{n}+2{b}_{n}}$化简,利用等比数列的定义即可证明;
(2)由(1)和等比数列的通项公式求出an和bn,利用指数函数的单调性判断出两个数列的单调性,以及满足条件的不等式和c的值,令$\left\{\begin{array}{l}{\frac{1342}{{4}^{n-1}}<1}\\{\frac{671}{{4}^{n-1}}<1}\end{array}\right.$求出n的值进一步证明,即可得到结论.
解答 证明:(1)∵对任意的正整数n,an,an+1,bn和an+1,bn+1,bn均成等差数列,
∴$\left\{\begin{array}{l}{{a}_{n+1}=\frac{{a}_{n}+{b}_{n}}{2}}\\{{b}_{n+1}=\frac{{a}_{n+1}+{b}_{n}}{2}}\end{array}\right.$,则$\left\{\begin{array}{l}{{a}_{n+1}=\frac{1}{2}{a}_{n}+\frac{1}{2}{b}_{n}}\\{{b}_{n+1}=\frac{1}{4}{a}_{n}+\frac{3}{4}{b}_{n}}\end{array}\right.$,
∴$\frac{{a}_{n+1}-{b}_{n+1}}{{a}_{n}-{b}_{n}}$=$\frac{(\frac{1}{2}{a}_{n}+\frac{1}{2}{b}_{n})-(\frac{1}{4}{a}_{n}+\frac{3}{4}{b}_{n})}{{a}_{n}-{b}_{n}}$=$\frac{1}{4}$,
又a1-b1=2-2015=-2013,
∴数列{an-bn}是以-2013为首项、$\frac{1}{4}$为公比的等比数列,
∵$\frac{{a}_{n+1}+2{b}_{n+1}}{{a}_{n}+2{b}_{n}}$=$\frac{(\frac{1}{2}{a}_{n}+\frac{1}{2}{b}_{n})+2(\frac{1}{4}{a}_{n}+\frac{3}{4}{b}_{n})}{{a}_{n}+2{b}_{n}}$=1,
又a1+2b1=2+4030=4032,
∴数列{an+2bn}是以4032为首项、1为公比的等比数列;
(2)由(1)可得,$\left\{\begin{array}{l}{{a}_{n}-{b}_{n}=-2013•\frac{1}{{4}^{n-1}}}\\{{{a}_{n}+2b}_{n}=4032}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{a}_{n}=1344-\frac{1342}{{4}^{n-1}}}\\{{b}_{n}=1344+\frac{671}{{4}^{n-1}}}\end{array}\right.$,
∴数列{an}是单调递增数列,数列{bn}是单调递减数列,且an<1344<bn,
∴存在唯一的正整数c=1344,使得an<c<bn恒成立,
令$\left\{\begin{array}{l}{\frac{1342}{{4}^{n-1}}<1}\\{\frac{671}{{4}^{n-1}}<1}\end{array}\right.$,解得22n-2>1342,则2n-2≥11,解得n≥6.5,
∴对任意的正整数n≥7时,有1343<an<1344<bn<1345,
且存在唯一的正整数c=1344,
综上所述,存在唯一的正整数c=1344,有an<1344<bn恒成立.
点评 本题考查等差中项的性质,等比数列的定义、通项公式,以及等比数列与函数的单调性关系,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
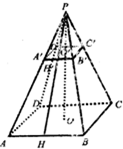 如图所示,正四棱锥P-ABCD被过棱锥高上O′点且平行底面的平面A′B′C′D′所截,得到正四棱台OO′和较小的棱锥PO′,其中O′分PO为$\frac{PO′}{OO′}$=$\frac{1}{2}$,侧棱PA长为15cm,小棱锥底面边长A′B′为6cm.
如图所示,正四棱锥P-ABCD被过棱锥高上O′点且平行底面的平面A′B′C′D′所截,得到正四棱台OO′和较小的棱锥PO′,其中O′分PO为$\frac{PO′}{OO′}$=$\frac{1}{2}$,侧棱PA长为15cm,小棱锥底面边长A′B′为6cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com