
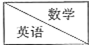
 | 优 | 良 | 及格 | 不及格 |
| 优 | 1 | 3 | 1 | 1 |
| 良 | 1 | 0 | 7 | 6 |
| 及格 | 2 | 4 | 0 | 9 |
| 不及格 | 1 | b | 7 | a+4 |
分析 (1)记数学及格且英语良为事件A,由题中表格知数学及格且英语良的人数为7人,根据概率公式计算即可得到答案;
(2)数学及格的共有15人,其中英语良的7人,即可求出在数学及格的条件下,英语良的概率;
(3)记数学良为事件B,英语不及格为事件C,分别求出P(B),P(C),再根据概率公式计算即可得到答案.
解答 解:(1)记数学及格且英语良为事件A,由题中表格知数学及格且英语良的人数为7人,
故P(A)=$\frac{7}{60}$…(3分)
(2)数学及格的共有15人,其中英语良的7人,
故数学及格的条件下,英语良的概率为$\frac{7}{15}$…(6分)
(3)表中所有数字和为a+b+47=60,
∴a+b=13,
记数学良为事件B,英语不及格为事件C.则P(B)=$\frac{b+7}{60}$,P(C)=$\frac{a+b+12}{60}$=$\frac{5}{12}$,
P(BC)=$\frac{b}{60}$,B与C独立,故m=-3,
P(BC)=P(B)P(C),即$\frac{B+7}{60}$-$\frac{5}{12}$=$\frac{b}{60}$,
得b=5,a=8…(12分)
点评 本题考查了相互独立事件的乘法公式,考查了古典概型的概率加法公式,考查了学生的读取图表的能力,是中档题


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
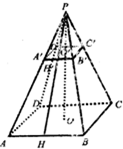 如图所示,正四棱锥P-ABCD被过棱锥高上O′点且平行底面的平面A′B′C′D′所截,得到正四棱台OO′和较小的棱锥PO′,其中O′分PO为$\frac{PO′}{OO′}$=$\frac{1}{2}$,侧棱PA长为15cm,小棱锥底面边长A′B′为6cm.
如图所示,正四棱锥P-ABCD被过棱锥高上O′点且平行底面的平面A′B′C′D′所截,得到正四棱台OO′和较小的棱锥PO′,其中O′分PO为$\frac{PO′}{OO′}$=$\frac{1}{2}$,侧棱PA长为15cm,小棱锥底面边长A′B′为6cm.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 将正偶数列{2n}中的所有项按每一行比上一行多一项的规则排成如图数表:记aij是这个数表的第i行第j列的数.例如a43=18.
将正偶数列{2n}中的所有项按每一行比上一行多一项的规则排成如图数表:记aij是这个数表的第i行第j列的数.例如a43=18.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
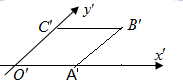 已知用斜二测画法得到四边形OABC的直观图是边长为2的菱形O′A′B′C′,如图所示,则四边形OABC的面积是( )
已知用斜二测画法得到四边形OABC的直观图是边长为2的菱形O′A′B′C′,如图所示,则四边形OABC的面积是( )| A. | 16 | B. | 8 | C. | 4 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com