Question

19．如图1，在直角梯形ABCD中，AB⊥BC，BC∥AD，AD=2AB=4，BC=3，E为AD中点，EF⊥BC，垂足为F．沿EF将四边形ABFE折起，连接AD，AC，BC，得到如图2所示的六面体ABCDEF．若折起后AB的中点M到点D的距离为3．

（Ⅰ）求证：平面ABFE⊥平面CDEF；
（Ⅱ）求六面体ABCDEF的体积．

Answer 1

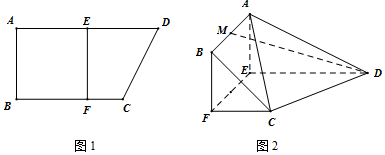
分析 （Ⅰ）取EF中点N，连接MN，DN，推导出四边形ABFE是边长为2的正方形，从而MN⊥EF，MN⊥DN，进而MN⊥平面CDEF，由此能证明平面ABFE⊥平面CDEF．
（Ⅱ）连接CE，V_{六面体ABCDEF}=V_{四棱锥C-ABFE}+V_{三棱锥A-CDE}．由此能求出六面体ABCDEF的体积．

解答 证明：（Ⅰ）取EF中点N，连接MN，DN．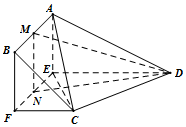
根据题意可知，四边形ABFE是边长为2的正方形，
∴MN⊥EF．
∵AD=2AB=4，BC=3，E为AD中点，EF⊥BC，垂足为F，
∴$DN=\sqrt{D{E^2}+E{N^2}}=\sqrt{5}$，∴$M{N^2}+D{N^2}={2^2}+{（\sqrt{5}）^2}=9=M{D^2}$，
∴MN⊥DN，EF∩DN=N，
∴MN⊥平面CDEF．
又∴MN?平面ABFE，∴平面ABFE⊥平面CDEF．…6分
解：（Ⅱ）连接CE，
则V_{六面体ABCDEF}=V_{四棱锥C-ABFE}+V_{三棱锥A-CDE}．
由（Ⅰ）的结论及CF⊥EF，AE⊥EF得，
CF⊥平面ABFE，AE⊥平面CDEF，
所以${V_{四棱锥C-ABFE}}=\frac{1}{3}•{S_{正方形ABFE}}•CF=\frac{4}{3}$，
${V_{三棱锥A-CDE}}=\frac{1}{3}•{S_{△CDE}}•AE=\frac{4}{3}$，
∴${V_{六面体ABCDEF}}=\frac{4}{3}+\frac{4}{3}=\frac{8}{3}$． …12分

点评 本题考查面面垂直的证明，考查六面体的体积的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．