
| A. | $({\frac{3}{2},\frac{5}{3}})$ | B. | $({\frac{5}{3},2})$ | C. | (2,3) | D. | $({\frac{3}{2},3})$ |
分析 设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)(a>b>0),其离心率e1,双曲线的方程为$\frac{{x}^{2}}{{m}^{2}}$-$\frac{{y}^{2}}{{n}^{2}}$=1(m>0,n>0),离心率为e2,由e1=$\frac{c}{a}$∈($\frac{3}{5}$,$\frac{2}{3}$),e2=$\frac{c}{m}$,由△PF1F2是以PF2为底边的等腰三角形,结合椭圆与双曲线的定义可求得m=2c-a,从而可求得答案.
解答 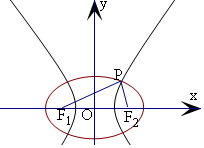 解:设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
解:设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
其离心率为e1,
双曲线的方程为$\frac{{x}^{2}}{{m}^{2}}$-$\frac{{y}^{2}}{{n}^{2}}$=1(m>0,n>0),其离心率为e2,
|F1F2|=2c,
∵有公共焦点的椭圆与双曲线在第一象限的交点为P,
△PF1F2是以PF2为底边的等腰三角形,
∴在椭圆中,|PF1|+|PF2|=2a,而|PF1|=|F1F2|=2c,
∴|PF2|=2a-2c,①
同理,在该双曲线中,|PF2|=2c-2m;②
由①②可得m=2c-a.
∵e1=$\frac{c}{a}$∈($\frac{3}{5}$,$\frac{2}{3}$),
∴$\frac{3}{2}$<$\frac{1}{{e}_{1}}$<$\frac{5}{3}$,
又e2=$\frac{c}{m}$=$\frac{c}{2c-a}$=$\frac{{e}_{1}}{2{e}_{1}-1}$=$\frac{1}{2-\frac{1}{{e}_{1}}}$∈(2,3).
故选:C.
点评 本题主要考查椭圆与双曲线的简单性质:离心率的范围,考查等价转换的思想与运算能力,考查倒数关系的灵活应用,属于中档题.


 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<-1或x≥1} | B. | {x|1≤x≤3或x<-1} | C. | {x|x≤-1或x>1} | D. | {x|1<x≤3或x≤-1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
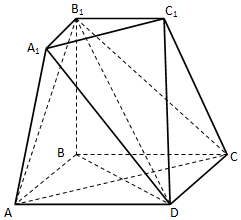 如图所示的几何体是由棱台ABC-A1B1C1和棱锥D-AA1C1C拼接而成的组合体,其底面四边形ABCD是边长为2的菱形,且∠BAD=60°,BB1⊥平面ABCD,BB1=2A1B1=2.(${V_{棱台}}=\frac{1}{3}h({{S_上}+{S_下}+\sqrt{{S_上}{S_下}}})$)
如图所示的几何体是由棱台ABC-A1B1C1和棱锥D-AA1C1C拼接而成的组合体,其底面四边形ABCD是边长为2的菱形,且∠BAD=60°,BB1⊥平面ABCD,BB1=2A1B1=2.(${V_{棱台}}=\frac{1}{3}h({{S_上}+{S_下}+\sqrt{{S_上}{S_下}}})$)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{10}{3}$ | C. | $\frac{7}{3}$ | D. | $\frac{8}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com