
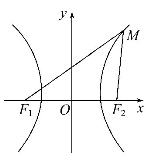
如图,设有双曲线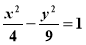 ,F1,F2是其两个焦点,点M在双曲线上.
,F1,F2是其两个焦点,点M在双曲线上.
(1)若∠F1MF2=90°,求△F1MF2的面积;
(2)若∠F1MF2=60°,△F1MF2的面积是多少?若∠F1MF2=120°,△F1MF2的面积又是多少?
(3)观察以上计算结果,你能看出随∠F1MF2的变化,△F1MF2的面积将怎样变化吗?试证明你的结论.
(1) 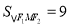 ; (2)
; (2) 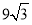 ,
, 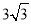 ; (3) θ增大时面积变小,证明过程见解析.
; (3) θ增大时面积变小,证明过程见解析.
【解析】
试题分析:(1) 设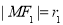 ,
,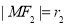 , 直角三角形△F1MF2中
, 直角三角形△F1MF2中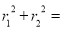
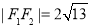 ,利用双曲线定义得
,利用双曲线定义得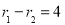 ,平方得
,平方得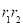 ,求得面积;(2) △F1MF2 中由余弦定理可得,|MF1|·|MF2|,由面积公式
,求得面积;(2) △F1MF2 中由余弦定理可得,|MF1|·|MF2|,由面积公式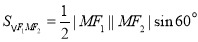 可得面积;(3) 由双曲线定义与余弦定理,可得面积与θ的关系
可得面积;(3) 由双曲线定义与余弦定理,可得面积与θ的关系 ,所以θ增大时面积变小.
,所以θ增大时面积变小.
【解析】
(1)由双曲线方程知a=2,b=3,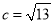 ,
,
设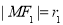 ,
,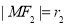 (
(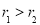 ).
).
由双曲线定义,有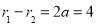 ,两边平方得,
,两边平方得,
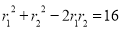 ,
,
即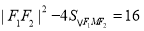 ,
,
也即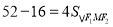 ,求得
,求得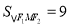 . 4分
. 4分
(2)若∠F1MF2=60°,在△MF1F2中,
由余弦定理得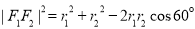 ,
,
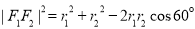 ,所以
,所以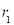
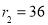 .
.
求得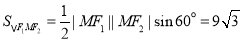 .
.
同理可求得若∠F1MF2=120°, 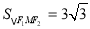 . 8分
. 8分
(3)由以上结果猜想,随着∠F1MF2的增大,△F1MF2的面积将减小.
证明如下:
令∠F1MF2=θ,则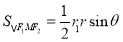 .
.
由双曲线定义及余弦定理,有
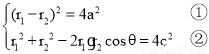
②-①得 ,
,
所以 ,
,
因为0<θ<π,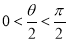 ,
,
在 内,
内,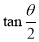 是增函数,
是增函数,
因此当θ增大时,  将减小. 12分
将减小. 12分
考点:双曲线的定义,余弦定理,三角形面积公式.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015届安徽省合肥六中高二下学期期末文数学试卷(解析版) 题型:选择题
已知数列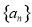 的前
的前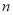 项和
项和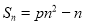 ,其中
,其中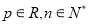 ,且
,且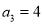 .则( )
.则( )
A.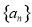 不是等差数列,且
不是等差数列,且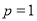
B.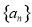 是等差数列,且
是等差数列,且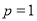
C.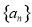 不是等差数列,且
不是等差数列,且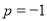
D.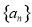 是等差数列,且
是等差数列,且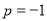
查看答案和解析>>
科目:高中数学 来源:2015届安徽师大附中高二下学期期中考查文科数学试卷(解析版) 题型:选择题
如果椭圆 的弦被点(4,2)平分,则这条弦所在的直线方程是 ( )
的弦被点(4,2)平分,则这条弦所在的直线方程是 ( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届宁夏高二下学期期中考试文科数学试卷(解析版) 题型:选择题
对于任意的两个实数对(a, b)和(c, d),规定(a, b)=(c, d)当且仅当a=c ,b=d;运算
“ ”为:
”为: ,运算“
,运算“ ”为:
”为:
 ,设
,设 ,若
,若
则 ( )
( )
A. B.
B.  C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届天津市红桥区高二下学期期中考试理科数学试卷(解析版) 题型:填空题
下表是关于新生婴儿的性别与出生时间段调查的列联表,那么,A= ,B= ,C= ,D= .
| 晚上 | 白天 | 总计 |
男 | 45 | A | 92 |
女 | B | 35 | C |
总计 | 98 | D | 180 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com