
分析 根据做差法比较即可.
解答 解:($\frac{y}{\sqrt{x}}$$-\sqrt{x}$)-($\sqrt{y}$$-\frac{x}{\sqrt{y}}$)
=$\frac{y-x}{\sqrt{x}}$-$\frac{y-x}{\sqrt{y}}$
=(y-x)($\frac{1}{\sqrt{x}}$-$\frac{1}{\sqrt{y}}$)
=$\frac{(\sqrt{y}-\sqrt{x})•(\sqrt{y}+\sqrt{x}+1)}{\sqrt{x}•\sqrt{y}}$,
∵x>0,y>0,x>y时,$\sqrt{y}$<$\sqrt{x}$,
$\frac{y}{\sqrt{x}}$$-\sqrt{x}$<$\sqrt{y}$$-\frac{x}{\sqrt{y}}$,
故答案为:$\frac{y}{\sqrt{x}}$$-\sqrt{x}$<$\sqrt{y}$$-\frac{x}{\sqrt{y}}$.
点评 本题考查了不等式的大小比较,是一道基础题.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
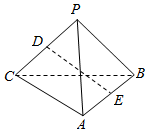 如图,P是平面ABC外一点,PA=4,BC=2$\sqrt{5}$,D,E分别为PC和AB的中点,且DE=3.求异面直线PA和BC所成角的大小.
如图,P是平面ABC外一点,PA=4,BC=2$\sqrt{5}$,D,E分别为PC和AB的中点,且DE=3.求异面直线PA和BC所成角的大小.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com