
 执行如图所示的程序框图.
执行如图所示的程序框图.分析 (Ⅰ)输入n=5时,程序执行5次循环,利用累加变量a=a+1求出输出a的值;
(Ⅱ)当输入n=100时,程序执行100次循环,
利用累加变量a=a+1,s=s+a,T=T+$\frac{1}{s}$和裂项法计算T的值.
解答 解:(Ⅰ)当输入n=5时,程序执行5次循环,
利用累加变量a=a+1,
计算输出a的值分别是:1,2,3,4,5;-------------------(5分)
(Ⅱ)当输入n=100时,程序执行100次循环,
利用累加变量a=a+1,s=s+a,T=T+$\frac{1}{s}$,
计算T=$\frac{1}{1}$+$\frac{1}{1+2}$+$\frac{1}{1+2+3}$+…+$\frac{1}{1+2+3+…+100}$
=1+2×($\frac{1}{2}$-$\frac{1}{3}$)+2×($\frac{1}{3}$-$\frac{1}{4}$)+…+2×($\frac{1}{100}$-$\frac{1}{101}$)
=1+2×($\frac{1}{2}$-$\frac{1}{101}$)
=$\frac{200}{101}$;---------------(10分)
故输出T的值为$\frac{200}{101}$.
点评 本题考查了程序框图与数列求和的应用问题,是较难的题目.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | e2x | B. | e2x-1 | C. | e2x-2 | D. | e2x-4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
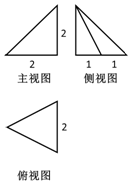
| A. | $\frac{4}{3}$ | B. | $7+\sqrt{5}$ | C. | $5+\sqrt{5}$ | D. | $7+2\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 2017年5月,印度电影《摔跤吧!爸爸》在中国上映,为了了解银川观众的满意度,某影院随机调查了本市观看影片的观众,现从调查人群中随机抽取13名,并用如图所示的茎叶图记录了他们的满意度分数(10分制,且以小数点前的一位数字为茎,小数点后的一位数字为叶).若分数不低于9分,则称该观众为“满意观众”.
2017年5月,印度电影《摔跤吧!爸爸》在中国上映,为了了解银川观众的满意度,某影院随机调查了本市观看影片的观众,现从调查人群中随机抽取13名,并用如图所示的茎叶图记录了他们的满意度分数(10分制,且以小数点前的一位数字为茎,小数点后的一位数字为叶).若分数不低于9分,则称该观众为“满意观众”.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com