
如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD,E、F分别是线段PA、CD的中点.
(Ⅰ)求证:PA⊥平面ABCD;
(Ⅱ)求EF和平面ABCD所成的角α的正切;
(Ⅲ)求异面直线EF与BD所成的角β的余弦.

(1)由已知PA⊥AD,AB⊥AD,所以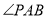 为平面PAD与平面ABCD所成二面角的平面角.
为平面PAD与平面ABCD所成二面角的平面角.
由已知平面PAD⊥平面ABCD得,PA⊥AB,又AB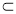 平面ABCD,AD
平面ABCD,AD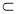 平面ABCD,且AB∩AD=A,所以PA⊥平面ABCD;(2)所求的角α的正切值为
平面ABCD,且AB∩AD=A,所以PA⊥平面ABCD;(2)所求的角α的正切值为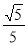 ;(3)异面直线EF与BD所成角β的余弦值为
;(3)异面直线EF与BD所成角β的余弦值为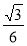 .
.
【解析】
试题分析:(1)根据两个平面垂直的性质定理可得PA⊥平面ABCD;(2)连接AF,则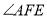 即为α,在直角三角形EAF中,根据
即为α,在直角三角形EAF中,根据 计算求得结果即可;(3))欲求异面直线EF与BD所成的角β的大小,只需平移两条异面直线中的一条,使它们成为相交直线,则相交直线所成的锐角或直角,就是异面直线所成角,再放入三角形中,通过解三角形,求出此角.
计算求得结果即可;(3))欲求异面直线EF与BD所成的角β的大小,只需平移两条异面直线中的一条,使它们成为相交直线,则相交直线所成的锐角或直角,就是异面直线所成角,再放入三角形中,通过解三角形,求出此角.
试题解析:(1)由已知PA⊥AD,AB⊥AD,所以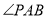 为平面PAD与平面ABCD所成二面角的平面角.
为平面PAD与平面ABCD所成二面角的平面角.
由已知平面PAD⊥平面ABCD得,PA⊥AB,又AB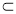 平面ABCD,AD
平面ABCD,AD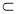 平面ABCD,且AB∩AD=A,所以PA⊥平面ABCD.
平面ABCD,且AB∩AD=A,所以PA⊥平面ABCD.
(2)连接AF,因为PA⊥平面ABCD,则AF是EF在平面ABCD上的射影,即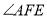 =α.设PA=AD=a,FD=
=α.设PA=AD=a,FD= ,则
,则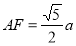 .在
.在 中,
中,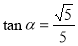 ,所以所求的角的正切值为
,所以所求的角的正切值为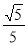 .
.
(3)取BC的中点M,连接EM、FM,则FM∥BD,∴∠EFM(或其补角)就是异面直线EF与BD所成的角.
可求得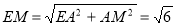 ,同理,
,同理,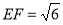 ,又
,又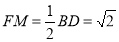 ,
,
∴在△MFE中,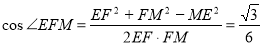 ,
,
故异面直线EF与BD所成角β的余弦值为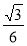 .
.
考点:异面直线及其所成的角;直线与平面平行、垂直的判定;直线与平面所成的角.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2015届广东省高二下学期中段考理科数学试卷(解析版) 题型:选择题
由数字0,1,2,3,4可组成无重复数字的两位数的个数是( )
A.25 B.20 C.16 D.12
查看答案和解析>>
科目:高中数学 来源:2015届广东省高二下学期期末考试理科数学试卷(解析版) 题型:选择题
一个袋中装有大小相同的5个白球和3个红球,现在不放回的取2次球,每次取出一个球,记“第1次拿出的是白球”为事件 ,“第2次拿出的是白球”为事件
,“第2次拿出的是白球”为事件 ,则事件
,则事件 与
与 同时发生的概率是( )
同时发生的概率是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届广东省高二下学期期末考试文科数学试卷(解析版) 题型:选择题
在复平面内,复数 对应的点位于( )
对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
查看答案和解析>>
科目:高中数学 来源:2015届广东省清远市高二下学期期末理科数学试卷(解析版) 题型:选择题
用数学归纳法证明12+32+52+…+(2n﹣1)2= n(4n2﹣1)过程中,由n=k递推到n=k+1时,不等式左边增加的项为( )
n(4n2﹣1)过程中,由n=k递推到n=k+1时,不等式左边增加的项为( )
A.(2k)2 B.(2k+3)2 C.(2k+2)2 D.(2k+1)2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com