
分析 (Ⅰ)利用极坐标与直角坐标互化方法,求曲线C的直角坐标方程;
(Ⅱ)直线l:$\left\{\begin{array}{l}{x=tcosα}\\{y=tsinα}\end{array}\right.$ 代入x2=4(1+y),可得t2cos2α=4(1+tsinα),即t2cos2α-4tsinα-4=0,利用参数的几何意义,结合韦达定理,求α的值.
解答 解:(Ⅰ)曲线C:ρ=$\frac{2}{1-sinθ}$,即ρ-ρsinθ=2,
∴ρ=2+ρsinθ,
∴x2+y2=(2+y)2,
即曲线C的直角坐标方程为x2=4(1+y);
(Ⅱ)直线l:$\left\{\begin{array}{l}{x=tcosα}\\{y=tsinα}\end{array}\right.$ 代入x2=4(1+y),
可得t2cos2α=4(1+tsinα),即t2cos2α-4tsinα-4=0
设A,B对应的参数分别为t1,t2,
则t1+t2=$\frac{4sinα}{co{s}^{2}α}$,①t1t2=-$\frac{4}{co{s}^{2}α}$②,
∵$\overrightarrow{OA}$+3$\overrightarrow{OB}$=$\overrightarrow{0}$,∴t1=-3t2,③
①②③联立可得$\frac{4}{\sqrt{3}cosα}$=$\frac{4sinα}{co{s}^{2}α}$,∴tanα=$\frac{\sqrt{3}}{3}$,
∵0≤α<π,∴α=$\frac{π}{6}$.
点评 本题考查极坐标与直角坐标互化方法,考查参数方程的运用,属于中档题.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | ||
| C. | 2个 | D. | a的值不同时零点的个数不同 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽六安一中高一上国庆作业二数学试卷(解析版) 题型:选择题
设函数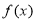 和
和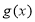 分别是
分别是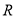 上的偶函数和奇函数,则下列结论恒成立的是( )
上的偶函数和奇函数,则下列结论恒成立的是( )
A.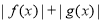 是偶函数 B.
是偶函数 B.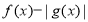 是奇函数
是奇函数
C.  是偶函数 D.
是偶函数 D.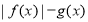 是奇函数
是奇函数
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com