
| x | 3 | -2 | $\sqrt{2}$ |
| y | -2$\sqrt{3}$ | 0 | $\frac{\sqrt{6}}{2}$ |
���� ��������Բ�ı�����Ϊ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0���������ߵķ�����Ϊy2=mx����m��0�����ɵõ㣨-2��0���͵㣨$\sqrt{2}$��$\frac{\sqrt{6}}{2}$������Բ�ϴ�����a��b�����ɵõ�������Բ���̣��ٽ��㣨3��-2$\sqrt{3}$�����������ߵķ��̣��ɵ�m�������õ������ߵķ��̣�
����i����M��x1��y1����N��x2��y2������$\left\{\begin{array}{l}{y=kx+m}\\{3{x}^{2}+4{y}^{2}=12}\end{array}\right.$����ȥy�������ã�3+4k2��x2+8kmx+4m2-12=0����ֱ��y=kx+m����Բ���������㣬֪m2��4k2+3����x1+x2=-$\frac{8km}{3+4{k}^{2}}$��֪MN�е�P�����꣬�ɴ������k�ķ�Χ��
��ii�������ҳ���ʽ�ɵ�|MN|����õ�O��ֱ��MN�ľ��룬���������ε������ʽ�������������ɵõ�����
��� �⣺��I������������Բ�ı�����Ϊ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����
�����ߵķ�����Ϊy2=mx����m��0����
������������ɵõ㣨-2��0������Բ�ϣ�
����a=2������Բ�ϵĵ�ĺ�������[-2��2]�ڣ�
��㣨$\sqrt{2}$��$\frac{\sqrt{6}}{2}$������Բ�ϣ���$\frac{2}{4}$+$\frac{6}{4{b}^{2}}$=1��
���b=$\sqrt{3}$������Բ����Ϊ$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1��
�ɵ㣨3��-2$\sqrt{3}$�����������ϣ��ɵ�12=3m��
���m=4���������ߵķ���Ϊy2=4x��
����i����M��x1��y1����N��x2��y2��
��$\left\{\begin{array}{l}{y=kx+m}\\{3{x}^{2}+4{y}^{2}=12}\end{array}\right.$����ȥy��������
��3+4k2��x2+8kmx+4m2-12=0��
ֱ��y=kx+m����Բ���������㣬�ɵ�
��=��8km��2-4��3+4k2����4m2-12����0����m2��4k2+3����
��x1+x2=-$\frac{8km}{3+4{k}^{2}}$��x1x2=$\frac{4{m}^{2}-12}{3+4{k}^{2}}$��
MN�е�P������Ϊ��-$\frac{4km}{3+4{k}^{2}}$��$\frac{3m}{3+4{k}^{2}}$����
��MN�Ĵ�ֱƽ����l'���̣�y=-$\frac{1}{k}$��x-$\frac{1}{8}$����
��P��l'�ϣ��ɵ�$\frac{3m}{3+4{k}^{2}}$=-$\frac{1}{k}$��-$\frac{4km}{3+4{k}^{2}}$-$\frac{1}{8}$������4k2+8km+3=0��
�ɵ�m=-$\frac{3+4{k}^{2}}{8k}$��
����ʽ����ٵ�$\frac{��3+4{k}^{2}��^{2}}{64{k}^{2}}$��4k2+3��
��Ϊk2��$\frac{1}{20}$����k��$\frac{\sqrt{5}}{10}$��k��-$\frac{\sqrt{5}}{10}$��
��k��ȡֵ��ΧΪ��-�ޣ�-$\frac{\sqrt{5}}{10}$���ȣ�$\frac{\sqrt{5}}{10}$��+�ޣ���
��ii���ɣ�i���ɵ�|MN|=$\sqrt{1+{k}^{2}}$•$\sqrt{��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}}$
=$\sqrt{1+{k}^{2}}$•$\sqrt{\frac{64{k}^{2}{m}^{2}}{��3+4{k}^{2}��^{2}}-\frac{4��4{m}^{2}-12��}{3+4{k}^{2}}}$=$\sqrt{1+{k}^{2}}$•$\frac{4\sqrt{3}\sqrt{3+4{k}^{2}-{m}^{2}}}{3+4{k}^{2}}$��
��O��ֱ��MN�ľ���Ϊd=$\frac{|m|}{\sqrt{1+{k}^{2}}}$���ɵ�
��OMN�����ΪS��OMN=$\frac{1}{2}$d•|MN|=$\frac{1}{2}$|m|•$\frac{4\sqrt{3}\sqrt{3+4{k}^{2}-{m}^{2}}}{3+4{k}^{2}}$
=$\frac{1}{2}$•|-$\frac{3+4{k}^{2}}{8k}$|•$\frac{4\sqrt{3}\sqrt{3+4{k}^{2}-\frac{��3+4{k}^{2}��^{2}}{64{k}^{2}}}}{3+4{k}^{2}}$��
����ɵ�S��OMN=$\frac{\sqrt{3}}{32}$•$\frac{\sqrt{��3+4{k}^{2}����60{k}^{2}-3��}}{{k}^{2}}$��
���� ���⿼����Բ�������ߵķ��̵���ע�����ô���ϵ����������ֱ�߷��̺���Բ��������������Τ�ﶨ�����б�ʽ����0���Լ��е����깫ʽ����ֱ�ߴ�ֱ��������б��֮��Ϊ-1�����黯�����������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2$\sqrt{2}$ | B�� | 2$\sqrt{3}$ | C�� | 12 | D�� | $\sqrt{10}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
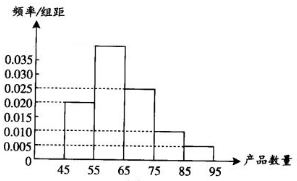 Ϊ�˵���ij����������ij�ֲ�Ʒ����������������20λ����ij�������ò�Ʒ����������Ʒ�����ķ�������Ϊ[45��55����[55��65����[65��75����[75��85����[85��95���ɴ˵õ�Ƶ�ʷֲ�ֱ��ͼ��ͼ�����Ʒ����λ��[55��65����Χ�ڵ�Ƶ��Ϊ0.4����20��������һ�������ò�Ʒ������[55��75����������13��
Ϊ�˵���ij����������ij�ֲ�Ʒ����������������20λ����ij�������ò�Ʒ����������Ʒ�����ķ�������Ϊ[45��55����[55��65����[65��75����[75��85����[85��95���ɴ˵õ�Ƶ�ʷֲ�ֱ��ͼ��ͼ�����Ʒ����λ��[55��65����Χ�ڵ�Ƶ��Ϊ0.4����20��������һ�������ò�Ʒ������[55��75����������13���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
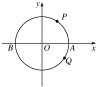 ��ͼ������P��Q�ӵ�A��3��0�������ơ�O��Բ���˶�������M����ʱ�뷽��ÿ����ת$\frac{��}{3}$rad����N��˳ʱ�뷽��ÿ����ת$\frac{��}{6}$rad����M��N��һ������ʱ����Mת���Ļ���Ϊ4�У�
��ͼ������P��Q�ӵ�A��3��0�������ơ�O��Բ���˶�������M����ʱ�뷽��ÿ����ת$\frac{��}{3}$rad����N��˳ʱ�뷽��ÿ����ת$\frac{��}{6}$rad����M��N��һ������ʱ����Mת���Ļ���Ϊ4�У��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{\sqrt{5}}{2}$ | B�� | $\frac{\sqrt{5}}{3}$ | C�� | $\frac{\sqrt{13}}{2}$ | D�� | $\frac{\sqrt{13}}{3}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com