
分析 (1)利用三角形内角和定理与两角和与差的正弦公式,即可求出sinAcosB的值;
(2)利用正弦定理把a=2b化为sinA=2sinB,再利用(1)的结论求出B的值,从而求出sinA的值.
解答 解:(1)△ABC中,A+B+C=π,
∴sin(A-B)+sinC=sin(A-B)+sin(A+B)
=(sinAcosB-cosAsinB)+(sinAcosB+cosAsinB)
=2sinAcosB=1,
∴sinAcosB=$\frac{1}{2}$;
(2)△ABC中,a=2b,
∴sinA=2sinB,
∴sinAcosB=2sinBcosB=sin2B=$\frac{1}{2}$,
∴2B=$\frac{π}{6}$或2B=$\frac{5π}{6}$,
∴B=$\frac{π}{12}$或B=$\frac{5π}{12}$;
∴sinB=$\frac{\sqrt{6}-\sqrt{2}}{4}$或sinB=$\frac{\sqrt{6}+\sqrt{2}}{4}$,
∴sinA=2sinB=$\frac{\sqrt{6}-\sqrt{2}}{2}$或sinA=2sinB=$\frac{\sqrt{6}+\sqrt{2}}{2}$(不合题意,舍去).
综上,sinA=$\frac{\sqrt{6}-\sqrt{2}}{2}$.
点评 本题考查了三角函数的恒等变换问题,也考查了正弦定理的应用问题,是综合性题目.


科目:高中数学 来源: 题型:选择题
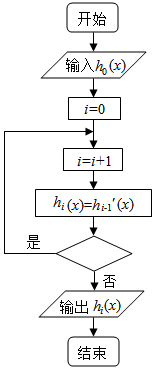 在如图所示的程序框图中(其中hi-1′(x)表示hi-1的导函数),当输入h0(x)=xex时,输出的hi(x)的结果是(x+2016)ex,则程序框图中的判断框内应填入( )
在如图所示的程序框图中(其中hi-1′(x)表示hi-1的导函数),当输入h0(x)=xex时,输出的hi(x)的结果是(x+2016)ex,则程序框图中的判断框内应填入( )| A. | i≤2014? | B. | i≤2015? | C. | i≤2016? | D. | i≤2017? |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20、8 | B. | 24、10 | C. | 10.5、24.5 | D. | 24.5、10.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{{\sqrt{3}+1}}{2}$,+∞) | B. | [$\frac{{\sqrt{3}+1}}{4}$,+∞) | C. | [$\frac{{\sqrt{3}-1}}{4}$,+∞) | D. | (-∞,$\frac{{\sqrt{3}-1}}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
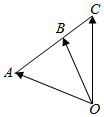 如图,$\overrightarrow{OA}$、$\overrightarrow{OB}$、$\overrightarrow{OC}$的终点A、B、C在一条直线上,且$\overrightarrow{AC}$=-3$\overrightarrow{CB}$,则以下等式成立的是( )
如图,$\overrightarrow{OA}$、$\overrightarrow{OB}$、$\overrightarrow{OC}$的终点A、B、C在一条直线上,且$\overrightarrow{AC}$=-3$\overrightarrow{CB}$,则以下等式成立的是( )| A. | $\overrightarrow{OC}$=-$\frac{1}{2}$$\overrightarrow{OA}$+$\frac{3}{2}$$\overrightarrow{OB}$ | B. | $\overrightarrow{OC}$=-$\overrightarrow{OA}$+2$\overrightarrow{OB}$ | C. | $\overrightarrow{OC}$=$\frac{3}{2}$$\overrightarrow{OA}$-$\frac{1}{2}$$\overrightarrow{OB}$ | D. | $\overrightarrow{OC}$=$\overrightarrow{OA}$-2$\overrightarrow{OB}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
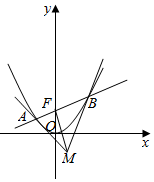 如图,已知F是抛物线x2=2py(p>0)的焦点,O为坐标原点,过点O、F的圆的圆心为Q,点Q到抛物线准线的距离为$\frac{3}{2}$.过点F的直线l交抛物线于A,B两点,过A,B分别作抛物线的切线,两切线交点为M.
如图,已知F是抛物线x2=2py(p>0)的焦点,O为坐标原点,过点O、F的圆的圆心为Q,点Q到抛物线准线的距离为$\frac{3}{2}$.过点F的直线l交抛物线于A,B两点,过A,B分别作抛物线的切线,两切线交点为M.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
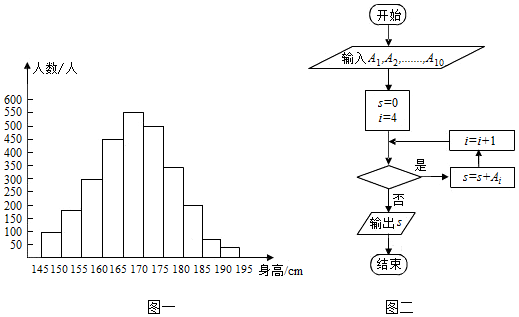
| A. | i<6?,1000 | B. | i<7?,1500 | C. | i<8?,1850 | D. | i<9?,2050 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com