
| A. | $\frac{{π+3\sqrt{3}}}{12}$ | B. | $\frac{{2π+3\sqrt{3}}}{6}$ | C. | $\frac{{2π+\sqrt{3}}}{12}$ | D. | $\frac{{2π+3\sqrt{3}}}{12}$ |
分析 若x,y∈R,则区域W的面积是2×2=4.满足|OM|≤2的点M构成的区域为{(x,y)|-1≤x≤1,0≤y≤2,x2+y2≤4},求出面积,即可求出概率.
解答 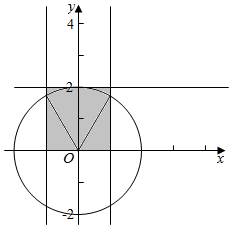 解:这是一个几何概率模型.
解:这是一个几何概率模型.
若x,y∈R,则区域W的面积是2×2=4.
满足|OM|≤2的点M构成的区域为{(x,y)|-1≤x≤1,0≤y≤2,
x2+y2≤4},
面积为2[$\frac{1}{4}π•{2}^{2}$-($\frac{1}{6}π•{2}^{2}$-$\frac{1}{2}×1×\sqrt{3}$)]=$\frac{2π}{3}$+$\sqrt{3}$,
故|OM|≤2的概率为$\frac{2π+3\sqrt{3}}{12}$.
故选:D.
点评 本题考查几何概率问题,确定满足|OM|≤2的点M构成的区域为{(x,y)|-1≤x≤1,0≤y≤2,x2+y2≤4},求出面积是关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,0] | B. | [-1,2] | C. | (1,2] | D. | (-∞,1]∪[2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 对于命题p:?x∈R,x2+x+1<0,则¬p:?x∈R,x2+x+1≥0 | |
| B. | 若p∧q为假命题,则p,q均为假命题 | |
| C. | 命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0” | |
| D. | “x>2”是“x2-3x+2>0”的充分不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com