
分析 (1)由tanα=2,利用弦化切公式求得cos2α的值;
(2)由(1)中求得的cos2α,结合平方关系求得sin2α,再由已知求得sinβ,结合两角差的正弦求得sin(2α-β),再由2α-β的范围求得答案.
解答 解:(1)∵tanα=2,∴cos2α=$\frac{1-ta{n}^{2}α}{1+ta{n}^{2}α}=\frac{1-4}{1+4}=-\frac{3}{5}$;
(2)由已知tanα=2,α∈(0,π),可得,α∈($\frac{π}{4},\frac{π}{2}$),
∴2α∈($\frac{π}{2},π$),则sin2α=$\sqrt{1-co{s}^{2}2α}=\frac{4}{5}$,
又cosβ=-$\frac{7\sqrt{2}}{10}$,且β∈(0,π),∴β∈($\frac{π}{2},π$),
∴sinβ=$\sqrt{1-co{s}^{2}β}$=$\sqrt{1-(-\frac{7\sqrt{2}}{10})^{2}}=\frac{\sqrt{2}}{10}$.
则sin(2α-β)=sin2αcosβ-cos2αsinβ=$\frac{4}{5}×(-\frac{7\sqrt{2}}{10})-(-\frac{3}{5})×\frac{\sqrt{2}}{10}=-\frac{\sqrt{2}}{2}$.
∵2α∈($\frac{π}{2},π$),β∈($\frac{π}{2},π$),
∴2α-β∈($-\frac{π}{2},\frac{π}{2}$),则2α-β=$-\frac{π}{4}$.
点评 本题考查三角函数中的恒等变换应用,考查了已知三角函数值求角,关键是对角范围的确定,是中档题.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:解答题
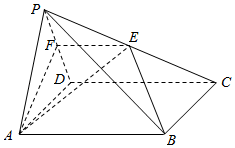 如图,在四棱锥P-ABCD中,底面ABCD是正方形.点E是棱PC的中点,平面ABE与棱PD交于点F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形.点E是棱PC的中点,平面ABE与棱PD交于点F.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | $-\frac{1}{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
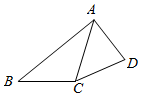 在平面四边形ABCD中,AB⊥AD,BC=1,cosB=$\frac{2\sqrt{7}}{7}$,∠ACB=$\frac{2π}{3}$.
在平面四边形ABCD中,AB⊥AD,BC=1,cosB=$\frac{2\sqrt{7}}{7}$,∠ACB=$\frac{2π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直线 | B. | 圆 | C. | 椭圆 | D. | 双曲线的一支 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=x2+2x+1 | B. | f(x)=-3x+2 | C. | f(x)=-x2+2x-4 | D. | f(x)=x+lnx-4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com