
已知双曲线的中心在原点,离心率为2,一个焦点为F(-2,0).
(1)求双曲线方程;
(2)设Q是双曲线上一点,且过点F,Q的直线l与y轴交于点M,若 = 2
= 2 ,求直线l的方程.
,求直线l的方程.
(1) 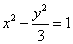
(2)y=± (x+2)或y=±
(x+2)或y=±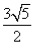 (x+2)
(x+2)
【解析】(1)由题意可设所求的双曲线方程为 ,
,
则有e= =2,c=2,所以a=1,则b=
=2,c=2,所以a=1,则b= ,
,
所以所求的双曲线方程为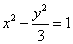 .
.
(2)因为直线l与y轴相交于M且过焦点F(-2,0),
所以l的斜率一定存在,设为k,则l:y=k(x+2),
令x=0,得M(0,2k),
因为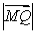 = 2
= 2 |M,Q,F共线于l,
|M,Q,F共线于l,
所以 = 2
= 2 或
或 = -2
= -2
当 =2
=2 时,
时, ,
, 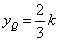 ,
,
所以Q的坐标(-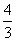 ,
,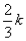 )
)
因为Q在双曲线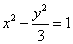 上,
上,
所以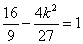 ,所以k=±
,所以k=± ,
,
所以直线l的方程为y=± (x+2).
(x+2).
当 = -2
= -2 时,
时,
同理求得Q(-4,-2k),代入双曲线方程得,
16- =1,所以k=±
=1,所以k=±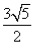 ,
,
所以直线l的方程为y=±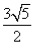 (x+2).
(x+2).
综上,所求的直线l的方程为y=± (x+2)或y=±
(x+2)或y=±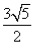 (x+2).
(x+2).


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源:2014高考名师推荐数学理科排列组合综合应用(解析版) 题型:选择题
从1,3,5,7,9这五个数中,每次取出两个不同的数分别记为a,b,共可得到lga-lgb的不同值的个数是( )
A.9
B.10
C.18
D.20
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学理科同角三角函数的基本关系式和诱导公式(解析版) 题型:选择题
已知tan ,
, 是关于x的方程x2-kx+k2-3=0的两个实根,且3π<
是关于x的方程x2-kx+k2-3=0的两个实根,且3π< <
< ,则cos
,则cos +sin
+sin = ( )
= ( )
A. 
B. 
C. -
D. -
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学理科双曲线(解析版) 题型:选择题
如图, 分别是双曲线C:
分别是双曲线C: 的左、右焦点,B是虚轴的端点,直线F1B与C的两条渐近线分别交于P,Q两点,线段PQ的垂直平分线与x轴交与点M,若|MF2|=|F1F2|,则C的离心率是( )
的左、右焦点,B是虚轴的端点,直线F1B与C的两条渐近线分别交于P,Q两点,线段PQ的垂直平分线与x轴交与点M,若|MF2|=|F1F2|,则C的离心率是( )

A.
B.
C.
D.
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学理科参数方程(解析版) 题型:解答题
已知动点P,Q都在曲线C:  (t为参数)上,对应参数分别为t=
(t为参数)上,对应参数分别为t=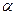 与t=2
与t=2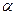 (0<
(0<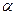 <2π),M为PQ的中点.
<2π),M为PQ的中点.
(1)求M的轨迹的参数方程;
(2)将M到坐标原点的距离d表示为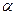 的函数,并判断M的轨迹是否过坐标原点.
的函数,并判断M的轨迹是否过坐标原点.
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学理科函数的奇偶性(解析版) 题型:填空题
设 是
是 上的奇函数,且
上的奇函数,且 ,下面关于
,下面关于 的判定:其中正确命题的序号为_______.
的判定:其中正确命题的序号为_______.
① ;
;
② 是以4为周期的函数;
是以4为周期的函数;
③ 的图象关于
的图象关于 对称;
对称;
④ 的图象关于
的图象关于 对称.
对称.
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学理科几何概型(解析版) 题型:填空题
随机地向区域 内投点,点落在区域的每一个位置是等可能的,则坐标原点与该点直线的倾斜角小于
内投点,点落在区域的每一个位置是等可能的,则坐标原点与该点直线的倾斜角小于 的概率为 .
的概率为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com