练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．不等式|x-1|+|x-2|≤5的解集为[-1，4]．

    分析 对x分x＜1，1≤x≤2与x＞2范围的讨论，去掉原不等式左端的绝对值符号，从而易解不等式|x-1|+|x-2|≤5的解集．

    解答 解：当x＜1时，|x-1|+|x-2|≤5?-x+1+2-x≤5，
    解得：-1≤x＜1；
    当1≤x≤2时，|x-1|+|x-2|≤5?x-1+2-x=1≤5恒成立，
    ∴1≤x≤2；
    当x＞2时，|x-1|+|x-2|≤5?x-1+x-2=2x-3≤5，
    解得：2＜x≤4．
    综上所述，不等式|x-1|+|x-2|≤5的解集为[-1，4]．
    故答案为：[-1，4]．

    点评 本题考查绝对值不等式的解法，去掉绝对值符号是关键，考查分类讨论思想与运算求解能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    8．已知：命题p：椭圆$\frac{{x}^{2}}{m+1}$+$\frac{{y}^{2}}{2-m}$=1的焦点在x轴上，命题q：不等式x2+2xy≤m（2x2+y2）对于一切整数x，y恒成立．
    （1）若p为假命题，求实数m的取值范围；
    （2）若p∧q是假命题，p∨q是真命题，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．${（1-\sqrt{x}）^5}$的展开式中x2的系数是（　　）
    A．-5B．5C．-10D．10

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．直线x-y-4=0上有一点P，它与两定点A（1，1）、B（2，3）的距离相等，则点P的坐标是（$\frac{9}{2}，\frac{1}{2}$）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．在四棱锥P-ABCD中，底面ABCD是直角梯形，AB∥DC，∠ABC=$\frac{π}{2}$，AD=2$\sqrt{2}$，AB=3DC=3．
    （1）在棱PB上确定一点E，使得CE∥平面PAD；
    （2）若PA=PD=$\sqrt{6}$，PB=PC，求直线PA与平面PBC所成角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知在△ABC中，a=2，∠A=$\frac{π}{3}$．
    （1）求面积的最大值；
    （2）求周长的最大值；
    （3）若三角形为锐角三角形，求周长的取值范围；
    （4）求b+2c的取值范围；
    （5）$\frac{sinB}{cosC}$＞$\sqrt{3}$，求∠C的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．如图是求$\frac{1}{1×2}$+$\frac{1}{3×4}$+$\frac{1}{5×6}$+…+$\frac{1}{101×102}$值的程序框图，回答下列问题．

    （1）该算法使用的是什么循环结构？
    （2）分别在①、②、③处填上合适的语句，使之能完成该题的算法功能．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．已知p：0≤2x-1≤7，q：x2-（2a+3）x+a2+3a≤0（a为常数），
    （Ⅰ）若p是q的充要条件，求a的值；
    （Ⅱ）若￢q是p的必要不充分条件，求a的范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

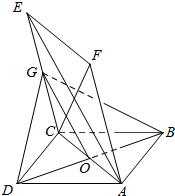    8．如图，已知边长为2的菱形ABCD与菱形ACEF全等，且∠FAC=∠ABC，平面ABCD⊥平面ACEF，点G为CE的中点．
    （Ⅰ）求证：AE∥平面DBG；
    （Ⅱ）求证：FC⊥BG；
    （Ⅲ）求三棱锥E-BGD的体积．

    查看答案和解析>>

    同步练习册答案