
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 ①,构造函数:f(x)=x-ln(x+1)(x>-1).利用导数求出单调区间,即可求出最值,就可判断;
②,取x=1,$\sqrt{x}$>-$\frac{{x}^{2}}{2}$+2x-$\frac{1}{2}$(x>0)不成立,;
③,构造函数g(x)=ln$\frac{1+x}{1-x}$-2(x+$\frac{{x}^{3}}{3}$)(x∈(0,1)),利用导数求出单调区间,即可求出最值,就可判断;
解答 解:对于①,x≥ln(x+1)(x>-1),构造函数:f(x)=x-ln(x+1)(x>-1).f′(x)=1-$\frac{1}{x+1}$=$\frac{x}{x+1}$,可得x∈(-1,0),函数f(x)递减,x∈(0,+∞)递增,故f(x)≥f(0)=0
∴x≥ln(x+1)(x>-1)成立,故$①\$成立.
对于②,取x=1,$\sqrt{x}$>-$\frac{{x}^{2}}{2}$+2x-$\frac{1}{2}$(x>0)不成立,故②不成立;
对于③,ln$\frac{1+x}{1-x}$>2(x+$\frac{{x}^{3}}{3}$)(x∈(0,1)),构造函数g(x)=ln$\frac{1+x}{1-x}$-2(x+$\frac{{x}^{3}}{3}$)(x∈(0,1)),
g′(x)=$\frac{1}{1+x}+\frac{1}{1-x}-2(1+{x}^{2})$=$\frac{{x}^{4}}{1-{x}^{2}}>$0,∴g(x)在(0,1)递增,而g(0)=0,故x∈(0,1)时,g(x)>0恒成立,故$③\\;成立$成立.
故选:B
点评 本题考查了构造函数,证明不等式,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 24-π | B. | 24-3π | C. | $8-\frac{4π}{3}$ | D. | $8-\frac{8π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $4\sqrt{3}$ | B. | 4 | C. | -4$\sqrt{3}$ | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,π) | B. | [0,$\frac{π}{4}$] | C. | [0,$\frac{π}{4}$]∪[$\frac{3π}{4}$,π) | D. | [0,$\frac{π}{4}$]∪($\frac{π}{2}$,$\frac{3π}{4}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
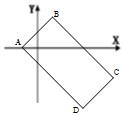 如图,已知复平面内平行四边形ABCD中,点A对应的复数为-1,$\overrightarrow{AB}$对应的复数为2+2i,$\overrightarrow{BC}$对应的复数为4-4i.
如图,已知复平面内平行四边形ABCD中,点A对应的复数为-1,$\overrightarrow{AB}$对应的复数为2+2i,$\overrightarrow{BC}$对应的复数为4-4i.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 推理形式错误 | B. | 大前提错误 | ||
| C. | 小前提错误 | D. | 大前提和小前提都错误 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com