
| A. | [0,10] | B. | [0,9] | C. | [2,10] | D. | [1,11] |
分析 由已知x,y满足的条件得到所求是在平行线之间的线段上的点中,求与原点距离最近和最远的距离.
解答 解:由题意,直线4x+3y=0过原点,并且x-y=-14与x-y=7平行,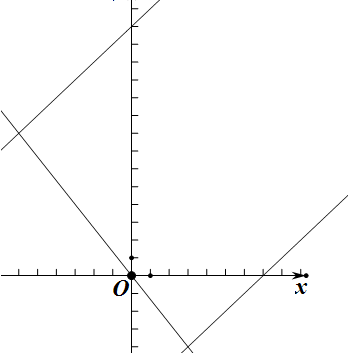 所以原点为使得$\sqrt{{x}^{2}+{y}^{2}}$的取值最小,为0;
所以原点为使得$\sqrt{{x}^{2}+{y}^{2}}$的取值最小,为0;
而直线4x+3y=0与x-y=-14交点距离原点最远,由$\left\{\begin{array}{l}{4x+3y=0}\\{x-y=-14}\end{array}\right.$得到交点(-6,8),所以
$\sqrt{{x}^{2}+{y}^{2}}$的取最大值为$\sqrt{(-6)^{2}+{8}^{2}}$=10;
所以$\sqrt{{x}^{2}+{y}^{2}}$的取值范围为:[0,10].
故选A.
点评 本题考查了简单线性规划;关键是从两个变量满足的条件入手,找到使得目标函数去最值的位置.


科目:高中数学 来源: 题型:选择题
| A. | $20\sqrt{6}$ | B. | 75 | C. | 51 | D. | 49 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 函数f(x)=Asin(ωx+φ)的图象如图所示,其中A>0,ω>0,|φ|<$\frac{π}{2}$,则下列关于函数f(x)的说法中正确的是( )
函数f(x)=Asin(ωx+φ)的图象如图所示,其中A>0,ω>0,|φ|<$\frac{π}{2}$,则下列关于函数f(x)的说法中正确的是( )| A. | 在(-$\frac{3π}{2}$,-$\frac{5π}{6}$)上单调递减 | B. | φ=-$\frac{π}{6}$ | ||
| C. | 最小正周期是π | D. | 对称轴方程是x=$\frac{π}{3}$+2kπ (k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
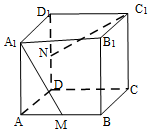 已知正方体ABCD-A1B1C1D1中,M,N分别为棱AB,DD1的中点,异面直线A1M和C1N所成的角为( )
已知正方体ABCD-A1B1C1D1中,M,N分别为棱AB,DD1的中点,异面直线A1M和C1N所成的角为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{2n+1}$ | B. | $\frac{2n}{2n+1}$ | C. | $\frac{n}{2n+1}$ | D. | $\frac{1}{2n+1}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com