
【题目】已知函数![]() .
.
⑴当![]() 时,求函数
时,求函数![]() 的极值;
的极值;
⑵若存在与函数![]() ,
,![]() 的图象都相切的直线,求实数
的图象都相切的直线,求实数![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 时,函数
时,函数![]() 取得极小值为
取得极小值为![]() ,无极大值;(2)
,无极大值;(2)![]()
【解析】试题分析:(1)![]() ,通过求导分析,得函数
,通过求导分析,得函数![]() 取得极小值为
取得极小值为![]() ,无极大值;(2)
,无极大值;(2)![]() ,所以
,所以![]() ,通过求导讨论,得到
,通过求导讨论,得到![]() 的取值范围是
的取值范围是![]() .
.
试题解析:
(1)函数![]() 的定义域为
的定义域为![]()
当![]() 时,
时,![]() ,
,
所以![]()
所以当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以函数![]() 在区间
在区间![]() 单调递减,在区间
单调递减,在区间![]() 单调递增,
单调递增,
所以当![]() 时,函数
时,函数![]() 取得极小值为
取得极小值为![]() ,无极大值;
,无极大值;
(2)设函数![]() 上点
上点![]() 与函数
与函数![]() 上点
上点![]() 处切线相同,
处切线相同,
则![]()
所以![]()
所以![]() ,代入
,代入![]() 得:
得:
![]()
设![]() ,则
,则![]()
不妨设![]() 则当
则当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
所以![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
代入![]() 可得:
可得:![]()
设![]() ,则
,则![]() 对
对![]() 恒成立,
恒成立,
所以![]() 在区间
在区间![]() 上单调递增,又
上单调递增,又![]()
所以当![]() 时
时![]() ,即当
,即当![]() 时
时![]() ,
,
又当![]() 时
时![]()
![]()
因此当![]() 时,函数
时,函数![]() 必有零点;即当
必有零点;即当![]() 时,必存在
时,必存在![]() 使得
使得![]() 成立;
成立;
即存在![]() 使得函数
使得函数![]() 上点
上点![]() 与函数
与函数![]() 上点
上点![]() 处切线相同.
处切线相同.
又由![]() 得:
得:![]()
所以![]() 单调递减,因此
单调递减,因此![]()
所以实数![]() 的取值范围是
的取值范围是![]() .
.


 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:
【题目】某中学为研究学生的身体素质与与课外体育锻炼时间的关系,对该校200名高三学生的课外体育锻炼平均每天运动的时间进行调查,如下表:(平均每天锻炼的时间单位:分钟)
将学生日均课外体育运动时间在![]() 上的学生评价为“课外体育达标”.
上的学生评价为“课外体育达标”.
平均每天锻炼的时间(分钟) |
|
|
|
|
|
|
总人数 | 20 | 36 | 44 | 50 | 40 | 10 |
请根据上述表格中的统计数据填写下面![]() 列联表,并通过计算判断是否能在犯错误的概率不超过
列联表,并通过计算判断是否能在犯错误的概率不超过![]() 的前提下认为“课外体育达标”与性别有关?
的前提下认为“课外体育达标”与性别有关?
课外体育不达标 | 课外体育达标 | 合计 | |
男 | |||
女 | 20 | 110 | |
合计 |
从上述200名学生中,按“课外体育达标”、“课外体育不达标”分层抽样,抽取4人得到一个样本,再从这个样本中抽取2人,求恰好抽到一名“课外体育不达标”学生的概率.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)求圆心在直线![]() 上,且与直线
上,且与直线![]() 相切于点
相切于点![]() 的圆的方程;
的圆的方程;
(2)求与圆![]() 外切于点
外切于点![]() 且半径为
且半径为![]() 的圆的方程.
的圆的方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:
(1)由题意可得圆的一条直径所在的直线方程为![]() ,据此可得圆心
,据此可得圆心![]() ,半径
,半径![]() ,则所求圆的方程为
,则所求圆的方程为![]() .
.
(2)圆的标准方程为![]() ,得该圆圆心为
,得该圆圆心为![]() ,半径为
,半径为![]() ,两圆连心线斜率
,两圆连心线斜率![]() .设所求圆心为
.设所求圆心为![]() ,结合弦长公式可得
,结合弦长公式可得![]() ,
,![]() .则圆的方程为
.则圆的方程为![]() .
.
试题解析:
(1)过点![]() 且与直线
且与直线![]() 垂直的直线为
垂直的直线为![]() ,
,
由![]()
![]() .
.
即圆心![]() ,半径
,半径![]() ,
,
所求圆的方程为![]() .
.
(2)圆方程化为![]() ,得该圆圆心为
,得该圆圆心为![]() ,半径为
,半径为![]() ,故两圆连心线斜率
,故两圆连心线斜率![]() .设所求圆心为
.设所求圆心为![]() ,
,
![]() ,∴
,∴![]() ,
,
![]() ,∴
,∴![]() .
.
∴![]() .
.
点睛:求圆的方程,主要有两种方法:
(1)几何法:具体过程中要用到初中有关圆的一些常用性质和定理.如:①圆心在过切点且与切线垂直的直线上;②圆心在任意弦的中垂线上;③两圆相切时,切点与两圆心三点共线.
(2)待定系数法:根据条件设出圆的方程,再由题目给出的条件,列出等式,求出相关量.一般地,与圆心和半径有关,选择标准式,否则,选择一般式.不论是哪种形式,都要确定三个独立参数,所以应该有三个独立等式.
【题型】解答题
【结束】
20
【题目】如图所示,![]() 平面
平面![]() ,点
,点![]() 在以
在以![]() 为直径的
为直径的![]() 上,
上,![]() ,
,![]() ,点
,点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 在弧
在弧![]() 上,且
上,且![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)设二面角![]() 的大小为
的大小为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为实常数).
为实常数).
(1)若![]() ,写出
,写出![]() 的单调递增区间(直接写结果)
的单调递增区间(直接写结果)
(2)若![]() ,设
,设![]() 在区间
在区间![]() 的最小值为
的最小值为![]() ,求
,求![]() 的表达式;
的表达式;
(3)设![]() ,若函数
,若函数![]() 在区间
在区间![]() 上是增函数,求实数
上是增函数,求实数![]() 的取值范围.
的取值范围.
参考结论:函数![]() (
(![]() 为常数),
为常数),![]() 时,
时,![]() 在
在![]() 上递增;
上递增;![]() 时,
时,![]() 在
在![]() 上递减,
上递减,![]() 上递增.
上递增.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量主要受污染物排放量及大气扩散等因素的影响,某市环保监测站2014年10月连续10天(从左到右对应1号至10号)采集该市某地平均风速及空气中氧化物的日均浓度数据,制成散点图如图所示.
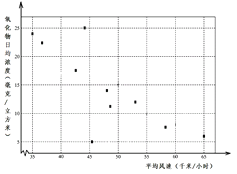
(Ⅰ)同学甲从这10天中随机抽取连续5天的一组数据,计算回归直线方程.试求连续5天的一组数据中恰好同时包含氧化物日均浓度最大与最小值的概率;
(Ⅱ)现有30名学生,每人任取5天数据,对应计算出30个不同的回归直线方程.已知30组数据中有包含氧化物日均浓度最值的有14组.现采用这30个回归方程对某一天平均风速下的氧化物日均浓度进行预测,若预测值与实测值差的绝对值小于2,则称之为“拟合效果好”,否则为“拟合效果不好”.根据以上信息完成下列2×2联表,并分析是否有95%以上的把握说拟合效果与选取数据是否包含氧化物日均浓度最值有关.
预测效果好 | 拟合效果不好 | 合计 | |
数据有包含最值 | 5 | ||
数据无包含最值 | 4 | ||
合计 |
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
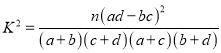 (其中
(其中![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2-2x-3≤0},B={x|x2-2mx+m2-4≤0,x∈R,m∈R}.
(1)若A∩B=[0,3],求实数m的值;
(2)若ARB,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com