
分析 ①S=∫${\;}_{0}^{4}$$\frac{1}{4}$(x-4)2dx即可求解面积,
②求解dy=$\frac{1}{2}$(x-4)dx,dl=dx$•\sqrt{1+\frac{1}{4}(x-4)^{2}}$=$\frac{1}{2}\sqrt{4+(x-4)^{2}}$dx,
运用积分求解弧长$\widehat{AB}$=∫${\;}_{0}^{4}$$\frac{1}{2}\sqrt{4+(x-4)^{2}}$dx即可求解周长.
解答 解:①∵函数y=$\frac{1}{4}$(x-4)2
∴S=∫${\;}_{0}^{4}$$\frac{1}{4}$(x-4)2dx=[$\frac{1}{12}$(x-4)3]${\;}_{0}^{4}$=$\frac{16}{3}$
C=8$+\widehat{AB}$,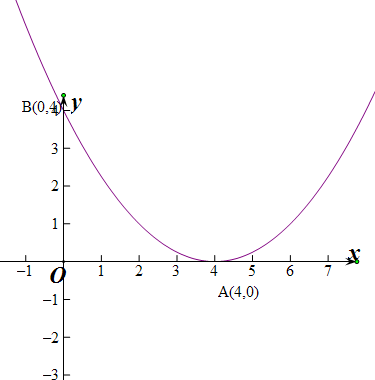
∵y=$\frac{1}{4}$(x-4)2,
∴dy=$\frac{1}{2}$(x-4)dx,
dl=dx$•\sqrt{1+\frac{1}{4}(x-4)^{2}}$=$\frac{1}{2}\sqrt{4+(x-4)^{2}}$dx,
∴$\widehat{AB}$=∫${\;}_{0}^{4}$$\frac{1}{2}\sqrt{4+(x-4)^{2}}$dx=$\frac{1}{2}\{\frac{x-4}{2}\sqrt{4+(x-4)^{2}}+2ln[(x-4)+\sqrt{4+(x-4)^{2}}]\}$${\;}_{0}^{4}$
=ln2-[-2$\sqrt{5}$$+ln(2\sqrt{5}-4)$]=2$\sqrt{5}$$+ln(2+\sqrt{5})$
∴周长C=8+2$\sqrt{5}$$+ln(2+\sqrt{5})$
故坐标轴围成的面积$\frac{16}{3}$和周长8+2$\sqrt{5}$$+ln(2+\sqrt{5})$
点评 本题考查了导数,积分的概念,几何意义的运用,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
 如图,在三棱锥P-ABC中,底面△ABC是边长为2的等边三角形,∠PCA=90°,E,F分别为AP,AC的中点,且PA=4,$BE=\sqrt{3}$.
如图,在三棱锥P-ABC中,底面△ABC是边长为2的等边三角形,∠PCA=90°,E,F分别为AP,AC的中点,且PA=4,$BE=\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | (2,+∞) | C. | (-2,0) | D. | (-2,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1-i | B. | 1+i | C. | -1-i | D. | -1+i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2$\sqrt{2}$ | C. | 2 | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com