
分析 (1)由T=$\frac{2π}{ω}$=π,得ω=2
(2)由(1)可知,f($\frac{A}{2}-\frac{π}{6}$)=2cosA=1,得$cosA=\frac{1}{2}$,$sinA=\frac{\sqrt{3}}{2}$,又$a=\frac{{\sqrt{3}}}{2}b$,且$\frac{a}{sinA}=\frac{b}{sinB}$,可得sinB=$\frac{bsinA}{a}$.
解答 解:(1)∵T=$\frac{2π}{ω}$=π,∴ω=2
(2)由(1)可知,f($\frac{A}{2}-\frac{π}{6}$)=2cosA=1,
∴$cosA=\frac{1}{2}$
∵0<A<π,∴$sinA=\frac{\sqrt{3}}{2}$
又$a=\frac{{\sqrt{3}}}{2}b$,且$\frac{a}{sinA}=\frac{b}{sinB}$,
所以sinB=$\frac{bsinA}{a}$=$\frac{2}{\sqrt{3}}×\frac{\sqrt{3}}{2}=1$
点评 本题考查了三角函数的性质,正弦定理的应用,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若直线l1与l2斜率相等,则l1∥l2 | |
| B. | 若直线l1∥l2,则k1=k2 | |
| C. | 若直线l1,l2的斜率不存在,则l1∥l2 | |
| D. | 若两条直线的斜率不相等,则两直线不平行 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{\sqrt{5}}{5}$) | B. | ($\frac{\sqrt{5}}{5}$,1) | C. | ($\frac{\sqrt{3}}{5}$,1) | D. | (0,$\frac{\sqrt{3}}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
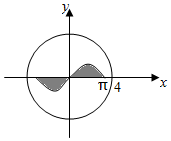 如图,圆O:x2+y2=16内的正弦曲线y=sinx,x∈[-π,π]与x轴围成的区域记为M(图中阴影部分),随机向圆O内投一个点P,记A表示事件“点P落在一象限”,B表示事件“点P落在区域M内”,则概率P(B|A)=$\frac{1}{2π}$.
如图,圆O:x2+y2=16内的正弦曲线y=sinx,x∈[-π,π]与x轴围成的区域记为M(图中阴影部分),随机向圆O内投一个点P,记A表示事件“点P落在一象限”,B表示事件“点P落在区域M内”,则概率P(B|A)=$\frac{1}{2π}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com