
分析 先得到x>1,a>1或0<x<1,0<a<1,从而${log}_{a}^{x}$>0,将不等式转化为(2${log}_{a}^{x}$-1)(${log}_{a}^{x}$-4)>0,求出${log}_{a}^{x}$的值,再分别讨论x>1,a>1或0<x<1,0<a<1的情况,从而求出x的范围.
解答 解:显然x>0且x≠1,a>0且a≠1,
x>1,0<a<1时,${log}_{a}^{x}$<0,x${\;}^{lo{g}_{a}x}$<1,而$\frac{{x}^{4}\sqrt{x}}{{a}^{2}}$>1,不等式无解,
同理0<x<1,a>1时,不等式无解,
故x>1,a>1或0<x<1,0<a<1,
a>1时:
由x${\;}^{lo{g}_{a}x}$>$\frac{{x}^{4}\sqrt{x}}{{a}^{2}}$得:${log}_{a}^{x}$>${log}_{x}^{\frac{{x}^{4}\sqrt{x}}{{a}^{2}}}$=$\frac{{log}_{a}^{{x}^{\frac{9}{2}}}{-log}_{a}^{{a}^{2}}}{{log}_{a}^{x}}$=$\frac{{\frac{9}{2}log}_{a}^{x}-2}{{log}_{a}^{x}}$,
∴${{(log}_{a}^{x})}^{2}$>$\frac{9}{2}$${log}_{a}^{x}$-2,
即2${{(log}_{a}^{x})}^{2}$-9${log}_{a}^{x}$+4>0,
∴(2${log}_{a}^{x}$-1)(${log}_{a}^{x}$-4)>0,
解得:${log}_{a}^{x}$<$\frac{1}{2}$或${log}_{a}^{x}$>4,
∴1<x<$\sqrt{a}$或x>a4,
同理,0<a<1时:
$\sqrt{a}$<x<1或0<x<a4.
点评 本题考察了指数、对数的互化,以及解对数不等式问题,是一道中档题.


科目:高中数学 来源: 题型:解答题
| 分组 | 频数 | 频率 |
| [1200,1800) | x | A |
| [1800,2400) | 90 | B |
| [2400,3000) | y | 0.40 |
| [3000,3600) | 160 | 0.32 |
| [3600,4200] | z | 0.04 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
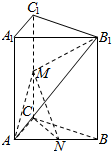 如图,已知三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AC=BC,M,N分别是棱CC1,AB的中点.
如图,已知三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AC=BC,M,N分别是棱CC1,AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{{e}_{1}}$=(-2,3),$\overrightarrow{{e}_{2}}$=(4,-6) | B. | $\overrightarrow{{e}_{1}}$=(1,5),$\overrightarrow{{e}_{2}}$=(-2,1) | ||
| C. | $\overrightarrow{{e}_{1}}$=(2,3),$\overrightarrow{{e}_{2}}$=(-1,-$\frac{3}{2}$) | D. | $\overrightarrow{{e}_{1}}$=(3,4),$\overrightarrow{{e}_{2}}$=(-6,-8) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
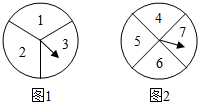 某校高一年级甲、已两班准备联合举行晚会,两班各派一人先进行转盘游戏,胜者获得一件奖品,负者表演一个节目.甲班的文娱委员利用分别标有数字1,2,3,4,5,6,7的两个转盘(如图所示),设计了一种游戏方案:两人同时各转动一个转盘一次,将转到的数字相加,和为偶数时甲班代表获胜,否则乙班代表获胜.
某校高一年级甲、已两班准备联合举行晚会,两班各派一人先进行转盘游戏,胜者获得一件奖品,负者表演一个节目.甲班的文娱委员利用分别标有数字1,2,3,4,5,6,7的两个转盘(如图所示),设计了一种游戏方案:两人同时各转动一个转盘一次,将转到的数字相加,和为偶数时甲班代表获胜,否则乙班代表获胜.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∨q | C. | ¬p∨q | D. | p∧¬q |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com