
 为了解学生身高情况,某校以8%的比例对全校1000名学生按性别进行分层抽样调查,已知男女比例为1:1,测得男生身高情况的频率分布直方图(如图所示):
为了解学生身高情况,某校以8%的比例对全校1000名学生按性别进行分层抽样调查,已知男女比例为1:1,测得男生身高情况的频率分布直方图(如图所示):分析 (1)由频率分布直方图能求出所抽取的男生的人数和中位数.
(2)样本中身高在[180,185)内的男生有4人,设为a,b,c,d,样本中身高在[185,190)内的有2人,设为e,f,利用列举法能出至少有1人身高在185~190cm之间的概率.
解答 解:(1)由题意得所抽取的男生的人数为:
1000×$8%×\frac{1}{2}=40$人,
设中位数为x,
依据样本频率分布直方图,得:0.01×5+0.025×5+x=0.5,
解x=0.325,
∵身高在[170,175)内的频率为0.35,
∴中位数为:170+5×$\frac{0.325}{0.35}$≈174.64(cm).
(2)样本中身高在[180,185)内的男生有4人,设为a,b,c,d,
样本中身高在[185,190)内的有2人,设为e,f,
从样本中身高在180~190cm之间的男生中任选2人,
基本事件总数n=15,分别为:
ab,ac,ad,ae,af,bc,bd,be,bf,cd,ce,cf,de,df,ef,
至少有1人身高在185~190cm之间包含的基本事件个数m=9,
∴至少有1人身高在185~190cm之间的概率p=$\frac{9}{15}=\frac{3}{5}$.
点评 本题考查抽取的男生人数、中位数、概率的求法,考查频率分布直方图、列举法等基础知识,考查数据处理能力、运算求解能力,考查数形结合思想、函数与方程思想,是基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
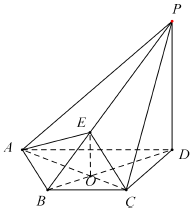 如图,在四棱锥P-ABCD中,PD⊥平面 ABCD,AC⊥BD于点O,E为线段PB 上的点,且BD⊥AE.
如图,在四棱锥P-ABCD中,PD⊥平面 ABCD,AC⊥BD于点O,E为线段PB 上的点,且BD⊥AE.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 6 | C. | 4 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com