
| A. | 2015 | B. | 2016 | C. | 4030 | D. | 4032 |
分析 特殊值法:令x1=x2=0,得f(0)=2016,再令x1+x2=0,将f(0)=2016代入可得f(x)+f(-x)=4032.根据条件x>0时,有f(x)<2016,得出函数的单调性,根据单调性求出函数的最值.
解答 解:∵对于任意的x1,x2∈[-2016,2016],都有f(x1+x2)=f(x1)+f(x2)-2016,
∴令x1=x2=0,得f(0)=2016,
再令x1+x2=0,将f(0)=2016代入可得f(x)+f(-x)=4032.
设x1<x2,x1,x2∈[-2016,2016],
则x2-x1>0,f(x2-x1)=f(x2)+f(-x1)-2016,
∴f(x2)+f(-x1)-2016<2016.
又∵f(-x1)=4032-f(x1),
∴f(x2)<f(x1),
即函数f(x)是递减的,
∴f(x)max=f(-2016),f(x)min=f(2016).
又∵f(2016)+f(-2016)=4032,
∴M+N的值为4032.
故选D.
点评 考查了抽象函数中特殊值的求解方法,得出函数的性质.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
 在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=60°,AC=CC1=2,BC=1,E,F分别是A1C1,BC的中点.
在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=60°,AC=CC1=2,BC=1,E,F分别是A1C1,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
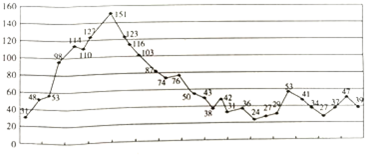
| 空气质量 指数类别 | 优 [0,35] | 良 (35,75] | 轻度污染 (75,115] | 中度污染 (115,150] | 重度污染 (150,250] | 严重污染 (250,500] | 合计 |
| 频数 | 30 | ||||||
| 频率 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com