练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．若函数f（x）=$\left\{\begin{array}{l}{{2}^{1-x}，x＜1}\\{1+lo{g}_{2}x，x≥1}\end{array}\right.$，则使得f（x）≤2成立的x的范围是[0，2]．

    分析 由分段函数，可得当x＜1时，21-x≤2，当x≥1时，1+log2x≤2，运用指数函数和对数函数的单调性，解不等式即可得到所求范围．

    解答 解：函数f（x）=$\left\{\begin{array}{l}{{2}^{1-x}，x＜1}\\{1+lo{g}_{2}x，x≥1}\end{array}\right.$，
    可得当x＜1时，f（x）≤2，即为21-x≤2，
    即1-x≤1，解得0≤x＜1；
    当x≥1时，1+log2x≤2，解得1≤x≤2．
    综上可得，x的范围是[0，2]．
    故答案为：[0，2]．

    点评 本题考查分段函数的运用：解不等式，注意运用指数函数和对数函数的单调性，考查运算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    9．已知向量$\overrightarrow a=（m，n），\overrightarrow b=（1，1）$，满足$\overrightarrow a•\overrightarrow b≥$2，且$\overrightarrow a（\overrightarrow a-2\overrightarrow b）≤0$，则$\overrightarrow a•\overrightarrow b$的取值范围是[2，4]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

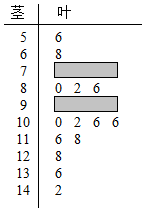    10．某校高三期中考试后，数学教师对本次全部数学成绩按1：20进行分层抽样，随机抽取了20名学生的成绩为样本，成绩用茎叶图记录如图所示，但部分数据不小心丢失，同时得到如表所示的频率分布表：
    分数段（分）[50，70）[70，90）[90，110）[110，130）[130，150）总计
    频数b
    频率a0.25
    （Ⅰ）求表中a，b的值及成绩在[90，110）范围内的个体数；
    （Ⅱ）从样本中成绩在[100，130）内的个体中随机抽取4个个体，设其中成绩在[100，110）内的个体数为X，求X的分布列及数学期望E（X）；
    （Ⅲ）若把样本各分数段的频率看作总体相应各分数段的概率，现从全校高三期中考试数学成绩中随机抽取3个，求其中恰好有1个成绩及格的概率（成绩在[90，150）内为及格）．
    附注：假定逐次抽取，且各次抽取互相独立．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知函数f（x）=|x-a|-|2x-1|．
    （1）当a=2时，求f（x）+3≥0的解集；
    （2）当x∈[1，3]时，f（x）≤3恒成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．设集合A={-2，-1，0，1，2}，集合B={y=|y=log${\;}_{\frac{1}{2}}$x，x≥1}，A∩B=（　　）
    A．{1，2}B．{-2，-1}C．{-2，-1，0}D．{1，2，0}

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知条件p：k=$\sqrt{3}$；条件q：直线y=kx+2与圆x2+y2=1相切，则￢p是￢q的（　　）
    A．充分必要条件B．必要不充分条件
    C．必要不充分条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．如图，在平行四边形ABCD中，AP⊥BD于点P，且$\overrightarrow{AP}$•$\overrightarrow{AC}$=18，则AP=3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．设函数f（x）=log7$\frac{x+3}{x-1}$，g（x）=log7（x-1）+log7（5-x），F（x）=f（x）+g（x）
    （1）求函数F（x）的定义域；
    （2）若F（a）＞1，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知函数$f（x）=Asin（wx+φ）（A＞0，w＞0，|φ|）＜\frac{π}{2}）$的图象的一个最高点的坐标为$（\frac{π}{6}，2）$，与其相邻的一个最低点的坐标为$（\frac{2π}{3}，-2）$
    （1）求函数f（x）的解析式；
    （2）求函数f（x）的单调增区间及对称轴方程．

    查看答案和解析>>

    同步练习册答案