
分析 由三角函数公式化简,由三角函数的最值和周期公式可得.
解答 解:化简可得f(x)=5sin2x+$\sqrt{3}$sinxcosx+6cos2x+m
=5sin2x+5cos2x+cos2x+$\sqrt{3}$sinxcosx+m
=5+$\frac{1}{2}$(1+cos2x)+$\frac{\sqrt{3}}{2}$sin2x+m
=$\frac{1}{2}$cos2x+$\frac{\sqrt{3}}{2}$sin2x+m+$\frac{11}{2}$
=sin(2x+$\frac{π}{6}$)+m+$\frac{11}{2}$
∴函数的最大值为1+m+$\frac{11}{2}$=1,解得m=-$\frac{11}{2}$,
由周期公式可得f(x)的最小正周期T=$\frac{2π}{2}$=π.
点评 本题考查三角函数恒等变换,属基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
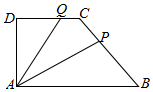 如图,在直角梯形ABCD中,AB∥CD,AB=2,AD=DC=1,P是线段BC上一动点,Q是线段DC上一动点,$\overrightarrow{DQ}=λ\overrightarrow{DC}$,$\overrightarrow{CP}=(1-λ)\overrightarrow{CB}$,若集合M=$\{x|x=\overrightarrow{AP}•\overrightarrow{AQ}\}$,N=$\left\{{x\left|{x=\frac{{{a^2}+{b^2}+1}}{3(a-b)},a>b,ab=1}\right.}\right\}$.则M∩N=[$\frac{2\sqrt{3}}{3}$,2].
如图,在直角梯形ABCD中,AB∥CD,AB=2,AD=DC=1,P是线段BC上一动点,Q是线段DC上一动点,$\overrightarrow{DQ}=λ\overrightarrow{DC}$,$\overrightarrow{CP}=(1-λ)\overrightarrow{CB}$,若集合M=$\{x|x=\overrightarrow{AP}•\overrightarrow{AQ}\}$,N=$\left\{{x\left|{x=\frac{{{a^2}+{b^2}+1}}{3(a-b)},a>b,ab=1}\right.}\right\}$.则M∩N=[$\frac{2\sqrt{3}}{3}$,2].查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com