
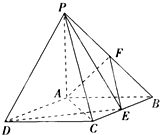
 如图所示,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=$\sqrt{3}$,点F是PB的中点,点E在棱BC上移动.
如图所示,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=$\sqrt{3}$,点F是PB的中点,点E在棱BC上移动.分析 (Ⅰ)当点E为BC的中点时,EF与平面PAC平行.由线面平行的判定定理可以证出结论.用线面平行的判定定理证明时要注意把条件写全.
(Ⅱ)建立空间坐标系设点E(x,1,0),求出用E的坐标表示的平面PDE的法向量,由线面角的向量表示公式建立方程求出E的坐标.
解答 解:(Ⅰ)当点E为BC的中点时,EF与平面PAC平行.
∵在△PBC中,E、F分别为BC、PB的中点,
∴EF∥PC.
又EF?平面PAC,而PC?平面PAC,
∴EF∥平面PAC.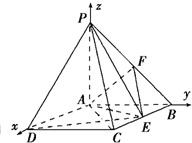
(Ⅱ)建立如图所示空间直角坐标系,则P(0,0,1),B(0,1,0),D($\sqrt{3}$,0,0),
设BE=x(0≤x≤$\sqrt{3}$),则E(x,1,0),
设平面PDE的法向量为$\overrightarrow{m}$=(p,q,1),
由$\left\{\begin{array}{l}\overrightarrow{m}•\overrightarrow{PD}=0\\ \overrightarrow{m}•\overrightarrow{DE}=0\end{array}\right.$,得$\left\{\begin{array}{l}\sqrt{3}p-r=0\\(x-\sqrt{3})p+q=0\end{array}\right.$,
令p=1,则$\overrightarrow{m}$=(1,$\sqrt{3}$-x,$\sqrt{3}$).
而$\overrightarrow{AP}$=(0,0,1),依题意PA与平面PDE所成角为45°,
所以sin45°=$\frac{\sqrt{2}}{2}$=$\frac{|\overrightarrow{m}•\overrightarrow{AP}|}{\left|\overrightarrow{m}\right|•\left|\overrightarrow{AP}\right|}$=$\frac{\sqrt{3}}{\sqrt{1+(\sqrt{3}-x)^{2}+3}}$,
解得BE=x=$\sqrt{3}-\sqrt{2}$或BE=x=$\sqrt{3}+\sqrt{2}$>$\sqrt{3}$(舍).
故BE=$\sqrt{3}-\sqrt{2}$时,PA与平面PDE所成角为45°.
点评 考查用向量证明立体几何中的问题,此类题的做题步骤一般是先建立坐标系,设出坐标,用线的方向向量的内积为0证线线垂直,线面垂直,用线的方向向量与面的法向量的垂直证面面平行,两者的共线证明线面垂直.此处为一规律性较强的题,要注意梳理清楚思路.


科目:高中数学 来源: 题型:选择题
| A. | (1,8) | B. | (1,7) | C. | (0,8) | D. | (8,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com