
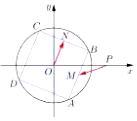
 如图,正方形ABCD内接于圆O:x2+y2=2,M,N分别为边AB,BC的中点,已知点P(2,0),当正方形ABCD绕圆心O旋转时,$\overrightarrow{PM}•\overrightarrow{ON}$的取值范围是( )
如图,正方形ABCD内接于圆O:x2+y2=2,M,N分别为边AB,BC的中点,已知点P(2,0),当正方形ABCD绕圆心O旋转时,$\overrightarrow{PM}•\overrightarrow{ON}$的取值范围是( )| A. | [-1,1] | B. | $[{-\sqrt{2},\sqrt{2}}]$ | C. | [-2,2] | D. | $[{-\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2}}]$ |
分析 由平面几何知识可得OM=ON,设M(cosα,sinα),用α表示出$\overrightarrow{PM}$和$\overrightarrow{ON}$,得到$\overrightarrow{PM}•\overrightarrow{ON}$关于α的函数,根据三角函数的性质得出答案.
解答 解:圆O的半径r=$\sqrt{2}$,∴正方形的边长为1,
∴OM=ON=1,设M(cosα,sinα),则N(cos($\frac{π}{2}+α$),sin($\frac{π}{2}+α$)),即N(-sinα,cosα),
∴$\overrightarrow{PM}$=(cosα-2,sinα),$\overrightarrow{ON}$=(-sinα,cosα),
∴$\overrightarrow{PM}•\overrightarrow{ON}$=2sinα-sinαcosα+sinαcosα=2sinα,
∵-1≤sinα≤1,∴-2≤2sinα≤2,
故选:C.
点评 本题考查了平面向量的数量积运算,三角函数的性质,属于中档题.


 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源: 题型:填空题
| X | 0 | 1 | 2 |
| P | a | $\frac{1}{2}$ | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,m∥β,则α∥β | B. | 若α∥β,m?α,n⊥β,则m⊥n | ||
| C. | 若m⊥α,m⊥n,则n∥α | D. | 若α⊥β,m?α,n⊥β,则m∥n |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,\frac{1}{2})$ | B. | (-∞,0)∪$(0,\frac{1}{2})$ | C. | $(\frac{1}{2},+∞)$ | D. | $(0,\frac{1}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 等边三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
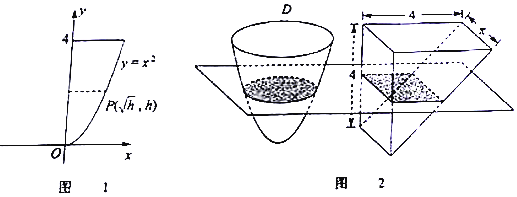
| A. | $\frac{16π}{3}$ | B. | 6π | C. | 8π | D. | 16π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com