
分析 先去绝对值号,原函数变成$y=\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}(x+2)}&{x>-2}\\{lo{g}_{\frac{1}{2}}[-(x+2)]}&{x<-2}\end{array}\right.$,分别分析每段函数和函数$lo{g}_{\frac{1}{2}}x$的关系,从而画出这两段函数,也就画出了原函数,根据函数图象即可写出其单调增区间.
解答 解:$y=lo{g}_{\frac{1}{2}}|x+2|=\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}(x+2)}&{x>-2}\\{lo{g}_{\frac{1}{2}}-(x+2)}&{x<-2}\end{array}\right.$;
$lo{g}_{\frac{1}{2}}(x+2)$是$lo{g}_{\frac{1}{2}}x$的图象向左平移2个单位得到;
$lo{g}_{\frac{1}{2}}[-(x+2)]$是先将$lo{g}_{\frac{1}{2}}x$关于y轴对称得到$lo{g}_{\frac{1}{2}}(-x)$,再将该函数图象向左平移2个单位便得到$lo{g}_{\frac{1}{2}}[-(x+2)]$的图象,所以原函数的图象如下所示: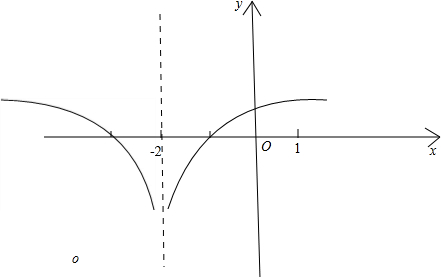 ∴由图象可以看出原函数的单调增区间为(-2,+∞).
∴由图象可以看出原函数的单调增区间为(-2,+∞).
点评 考查含绝对值函数的处理方法:去绝对值号,图象的平移变换及对称变换,熟悉对数函数的图象,以及根据函数图象判断函数的单调性.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±$\sqrt{2}$x | B. | y=±$\frac{{\sqrt{2}}}{2}$x | C. | y=±$\frac{1}{2}$x | D. | y=±2x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=$\frac{1}{x}$ | B. | f(x)=x+$\frac{1}{x}$ | C. | f(x)=(x-1)2 | D. | f(x)=ln(x+1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com