
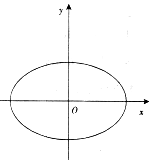
 ��֪��Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����ֱ��l��$\frac{x}{a}$-$\frac{y}{b}$=1����Բ��������e=$\frac{\sqrt{6}}{3}$������ԭ�㵽ֱ��l�ľ���Ϊ$\frac{\sqrt{3}}{2}$��
��֪��Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����ֱ��l��$\frac{x}{a}$-$\frac{y}{b}$=1����Բ��������e=$\frac{\sqrt{6}}{3}$������ԭ�㵽ֱ��l�ľ���Ϊ$\frac{\sqrt{3}}{2}$������ ��������Բ��������e=$\frac{\sqrt{6}}{3}$������ԭ�㵽ֱ��l��$\frac{x}{a}$-$\frac{y}{b}$=1�ľ���Ϊ$\frac{\sqrt{3}}{2}$�����a��b���ɴ��������Բ���̣�
����ֱ��m��б�ʲ�����ʱ��ֱ��m����Ϊx=0����CDΪֱ����Բ����E����ֱ��m��б�ʴ���ʱ����ֱ��m����Ϊy=kx+2����$\left\{{\begin{array}{l}{y=kx+2}\hfill\\{\frac{x^2}{3}+{y^2}=1}\hfill\end{array}}\right.$���ã�1+3k2��x2+12kx+9=0���ɴ����ø����б�ʽ��Τ�ﶨ����Բ�����ʣ������֪�������������CDΪֱ����Բ������Eʱ��ֱ��m�ķ��̣�
��� �⣺������ֱ��$l��\frac{x}{a}-\frac{y}{b}=1$����$\frac{{\sqrt{3}}}{2}=\frac{|ab|}{{\sqrt{{a^2}+{b^2}}}}$����4a2b2=3a2+3b2--��
����$e=\frac{{\sqrt{6}}}{3}$����$\frac{c^2}{a^2}=\frac{2}{3}$����${c^2}=\frac{2}{3}{a^2}$���֡�a2=b2+c2����${b^2}=\frac{1}{3}{a^2}$--��
���ڴ���ٵã���$\frac{4}{3}{a^4}=4{a^2}$����a2=3��b2=2��c2=1��
��������Բ������$\frac{x^2}{3}+{y^2}=1$��
���ٵ�ֱ��m��б�ʲ�����ʱ��ֱ��m����Ϊx=0��
��ֱ��m����Բ�Ľ���Ϊ��0����1�����֡�E��-1��0����
���CED=90�㣬����CDΪֱ����Բ����E��
�ڵ�ֱ��m��б�ʴ���ʱ����ֱ��m����Ϊy=kx+2��C��x1��y1����D��x2��y2����
��$\left\{{\begin{array}{l}{y=kx+2}\hfill\\{\frac{x^2}{3}+{y^2}=1}\hfill\end{array}}\right.$���ã�1+3k2��x2+12kx+9=0��
�ɡ�=144k2-4��9��1+3k2��=36k2-36��0����k��1��k��-1��
��${x_1}+{x_2}=\frac{-12k}{{1+3{k^2}}}$��${x_1}{x_2}=\frac{9}{{1+3{k^2}}}$��
��y1y2=��kx1+2����kx2+2��=k2x1x2+2k��x1+x2��+4
����CDΪֱ����Բ����E����EC��ED����$\overrightarrow{EC}•\overrightarrow{ED}=0$��
��$\overrightarrow{EC}=��{x_1}+1��{y_1}��$��$\overrightarrow{ED}=��{x_2}+1��{y_2}��$��
�ã�x1+1����x2+1��+y1y2=0���ࣨ1+k2��x1x2+��2k+1����x1+x2��+5=0��
��$\frac{{9��1+{k^2}��}}{{1+3{k^2}}}+��2k+1��•\frac{-12k}{{1+3{k^2}}}+5=0$�����$k=\frac{7}{6}��1$����$m��y=\frac{7}{6}x+2$��
��������������CDΪֱ����Բ������Eʱ��ֱ��m�ķ���Ϊx=0��$y=\frac{7}{6}x+2$��
���� ���⿼����Բ���̵�������������ֱ���Ƿ���ڵ��ж��������е��⣬����ʱҪ�������⣬ע����Բ�������б�ʽ��Τ�ﶨ����ֱ�����ʵĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 5 | C�� | -5 | D�� | ��5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
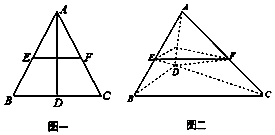 ��ͼһ���ڱ߳�Ϊ2�ĵȱ�������ABC�У�D��E��F�ֱ���BC��AB��AC���е㣬����ABD��AD���𣬵õ���ͼ����ʾ������A-BCD������$BC=\sqrt{2}$��
��ͼһ���ڱ߳�Ϊ2�ĵȱ�������ABC�У�D��E��F�ֱ���BC��AB��AC���е㣬����ABD��AD���𣬵õ���ͼ����ʾ������A-BCD������$BC=\sqrt{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����PΪԲE����x-1��2+y2=r2��r��1����x����㣬����P����PQ��ʹPQ��y�ύ��PQ���е�D��
��ͼ����PΪԲE����x-1��2+y2=r2��r��1����x����㣬����P����PQ��ʹPQ��y�ύ��PQ���е�D���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 30 | B�� | 25 | C�� | 20 | D�� | 15 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [-2��-1] | B�� | [-1��1] | C�� | [1��3] | D�� | [3��+��] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{3}{4}$ | B�� | $\frac{1}{2}$ | C�� | $\frac{{\sqrt{3}}}{2}$ | D�� | $\frac{{\sqrt{2}}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 8 | B�� | 4 | C�� | 1 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com