
分析 (1)利用平方和公式计算即可,
(2)由2lg$\frac{x-y}{2}$=lgx+lgy,先求出$\frac{x}{y}$的值,再代入即可
解答 解:(1)(a${\;}^{\frac{1}{2}}$+a${\;}^{-\frac{1}{2}}$)2=a+a-1+2=6,
∵a${\;}^{\frac{1}{2}}$+a${\;}^{-\frac{1}{2}}$>0,
∴a${\;}^{\frac{1}{2}}$+a${\;}^{-\frac{1}{2}}$=$\sqrt{6}$
(2)2lg$\frac{x-y}{2}$=lgx+lgy=lgxy,
∴(x-y)2=4xy,
即$\frac{y}{x}$+$\frac{x}{y}$=6,
解得$\frac{x}{y}$=3+2$\sqrt{2}$,或x=3-2$\sqrt{2}$(舍),
log${\;}_{(3-2\sqrt{2})}$$\frac{x}{y}$=log${\;}_{(3-2\sqrt{2})}$$\frac{1}{3-2\sqrt{2}}$=-1
点评 本题考查根式与分数指数幂的互化及其化简运算、对数的运算性质,解题时要认真审题,仔细解答,注意公式的灵活运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{2}{3}$,1] | B. | [0,1] | C. | [$\frac{2}{3}$,+∞) | D. | [1,+∞] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{1}{6}$,$\frac{1}{6}$] | B. | [-$\frac{\sqrt{6}}{6}$,$\frac{\sqrt{6}}{6}$] | C. | [-$\frac{1}{3}$,$\frac{1}{3}$] | D. | [-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 图象关于点$({-\frac{π}{6},0})$中心对称 | B. | 图象关于$x=-\frac{π}{6}$轴对称 | ||
| C. | 在区间$[{-\frac{5π}{12},-\frac{π}{6}}]$单调递增 | D. | 在$[{-\frac{π}{12},\frac{5π}{12}}]$单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
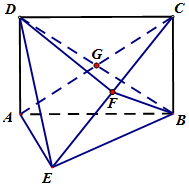 如图,矩形ABCD 中,AD⊥平面ABE,AE=FB=BC=2,F为CE上的点,且BF⊥平面ACE,AC,BD交于G点
如图,矩形ABCD 中,AD⊥平面ABE,AE=FB=BC=2,F为CE上的点,且BF⊥平面ACE,AC,BD交于G点查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com