
分析 由条件利用任意角的三角函数的定义,正弦函数的图象,正弦函数的单调性,得出结论.
解答 解:函数f(x)=Asin(2x+φ),其中角φ的终边经过点P(-l,1),
且0<φ<π,则tanφ=$\frac{1}{-1}$=-1,∴φ=$\frac{3π}{4}$.
再根据f($\frac{π}{2}$)=Asin(π+$\frac{3π}{4}$)=-Asin$\frac{3π}{4}$=-$\frac{\sqrt{2}}{2}$A=-2,∴A=2$\sqrt{2}$.
∴f(x)=2$\sqrt{2}$sin(2x+$\frac{3π}{4}$).
令2kπ+$\frac{π}{2}$≤2x+$\frac{3π}{4}$≤2kπ+$\frac{3π}{2}$,求得kπ-$\frac{π}{8}$≤x≤kπ+$\frac{3π}{8}$,k∈Z.
结合x∈[-$\frac{π}{2}$,$\frac{π}{2}$],可得减区间为[-$\frac{π}{8}$,$\frac{3π}{8}$],
故答案为:$\frac{3π}{4}$;2$\sqrt{2}$;[-$\frac{π}{8}$,$\frac{3π}{8}$].
点评 本题主要考查任意角的三角函数的定义,正弦函数的图象,正弦函数的单调性,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
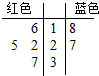 袋中有六张形状、质地等完全相同的卡片,其中红色卡片四张,蓝色卡片两张,每张卡片都标有一个数字,如茎叶图所示:
袋中有六张形状、质地等完全相同的卡片,其中红色卡片四张,蓝色卡片两张,每张卡片都标有一个数字,如茎叶图所示:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
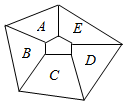 如图,在A,B,C,D,E五个区域中栽种3种植物,要求同一区域中只种1种植物,相邻两区域所种植物不同,则不同的栽种方法的总数为( )
如图,在A,B,C,D,E五个区域中栽种3种植物,要求同一区域中只种1种植物,相邻两区域所种植物不同,则不同的栽种方法的总数为( )| A. | 21 | B. | 24 | C. | 30 | D. | 48 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com