
分析 先分别求得∠A和∠B,进而求得∠C,利用正弦定理求得AB,最后除以时间.
解答  解:根据题意知∠BAC=15°+30°=45°,∠CBA=45°+60°=105°,∠C=180°-45°-105°=30°
解:根据题意知∠BAC=15°+30°=45°,∠CBA=45°+60°=105°,∠C=180°-45°-105°=30°
∴sin∠CBA=sin45°cos60°+cos45°sin60°=$\frac{\sqrt{2}}{2}$×$\frac{1}{2}$+$\frac{\sqrt{2}}{2}$×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{2}+\sqrt{6}}{4}$.
∴由正弦定理知$\frac{AC}{sinB}$=$\frac{AB}{sinC}$,
∴AB=$\frac{AC}{sinB}$•sinC=$\frac{20}{\frac{\sqrt{2}+\sqrt{6}}{4}}$×$\frac{1}{2}$=10($\sqrt{6}$$-\sqrt{2}$).
V=$\frac{AB}{t}$=$\frac{10(\sqrt{6}-\sqrt{2})}{\frac{1}{4}}$=40($\sqrt{6}$$-\sqrt{2}$)(海里/小时).
即货船的速度为40($\sqrt{6}$$-\sqrt{2}$)海里/小时.
故答案为:$40(\sqrt{6}-\sqrt{2})$.
点评 本题主要考查了正弦定理在解三角形中的应用.考查了学生分析问题和解决实际问题的能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≤-3或a≥-2 | B. | 2≤a≤3 | C. | a≤2或a≥3 | D. | -3≤a≤-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
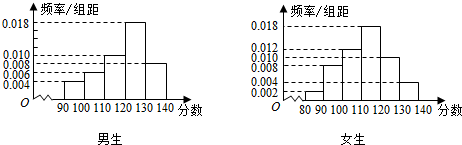
| 成绩性别 | 优秀 | 不优秀 | 总计 |
| 男生 | |||
| 女生 | |||
| 总计 |
| K0 | 2.072 | 2.076 | 3.814 | 5.024 | 6.635 | 7.879 | 10.828 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {a|-6≤a<2} | B. | {a|-4≤a<2}∪{-5}∪{-6} | C. | {a|-5≤a<2}∪{-6} | D. | {a|-4≤a<2}∪{-$\frac{14}{3}$}∪{-6} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
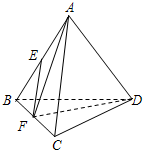
| A. | 异面直线AB与CD所成的角为90° | B. | 直线AB与平面BCD成的角为60° | ||
| C. | 直线EF∥平面ACD | D. | 平面AFD垂直平面BCD |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com