练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．若直线y=kx+1与直线2x-y+1=0垂直，则k的值为（　　）
    A．k=2B．k=-2C．$k=\frac{1}{2}$D．$k=-\frac{1}{2}$

    分析 根据两条直线垂直，它们的斜率之积等于-1，求出k的值．

    解答 解：∵直线y=kx+1与直线2x-y+1=0垂直，
    ∴2k=-1；$k=-\frac{1}{2}$．
    故选：D．

    点评 本题考查了两条直线垂直的判定与应用问题，解题时应用两直线垂直，斜率之积等于-1，是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    5．设全集U=R，已知集合M={x|x2-x＞0}，N={x|$\frac{x-1}{x}$＜0}，则有（　　）
    A．M∪N=RB．M∩N=∅C．CuN=MD．CvM⊆N

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．复数（1-4i）2的虚部为（　　）
    A．-4iB．-4C．-8iD．-8

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．已知|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=4，且$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{3}$，则$\overrightarrow{a}$•$\overrightarrow{b}$的值是（　　）
    A．2B．±2C．4D．±4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知等差数列{an}的前n项和记为Sn，公差为2，且a1，a2，a4依次构成等比数列．
    （1）求数列{an}的通项公式与Sn
    （2）数列{bn}满足bn=$\frac{1}{{S}_{n}}$，求数列{bn}的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．已知函数f（x）=2sin（ωx+θ ） （ω＞0）的图象如图所示，则ω=2，若将函数f（x）的图象向左平移φ $（{0＜φ＜\frac{π}{2}}）$个单位后得到一个偶函数，则φ=$\frac{π}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

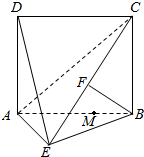    7．如图，四边形ABCD为矩形，AD⊥平面ABE，AE=EB=BC=2，F为CE上的点．且BF⊥平面ACE．
    （1）求证：平面ADE⊥平面BCE；
    （2）求二面角E-AC-B的大小；
    （3）设M在线段AB上，且满足AM=2MB，试在线段CE上确定一点N，使得MN∥平面DAE．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．已知sin（$\frac{π}{4}$+α）=$\frac{1}{3}$，α是第二象限角，则sin（2α+$\frac{5π}{6}$）=$\frac{4\sqrt{2}-7\sqrt{3}}{18}$或-$\frac{7\sqrt{3}+4\sqrt{2}}{18}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．设F1，F2是椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的左右焦点，若此椭圆上一点P满足|PF2|=|F1F2|，且原点O到直线PF1的距离不超过b，则离心率e的取值范围是（　　）
    A．（$\frac{1}{3}$，$\frac{{\sqrt{2}}}{2}$]B．（0，$\frac{5}{7}$]C．[$\frac{5}{7}$，1）D．（$\frac{1}{3}$，$\frac{5}{7}$]

    查看答案和解析>>

    同步练习册答案