
 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,M为棱AC中点.AB=BC,AC=2,AA1=$\sqrt{2}$.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,M为棱AC中点.AB=BC,AC=2,AA1=$\sqrt{2}$.分析 (Ⅰ)连结AB1交A1B于O,连结OM,可证OM∥B1C,又OM?平面A1BM,B1C?平面A1BM,即可证明B1C∥平面A1BM.
(Ⅱ)易证AA1⊥BM,又可证BM⊥AC1,由AC=2,AM=1,$A{A_1}=\sqrt{2}$,可求∠AC1C+∠C1AC=∠A1MA+∠C1AC=90°,从而可证A1M⊥AC1,从而证明AC1⊥平面A1BM.
(Ⅲ)当点N为BB1中点时,可证平面AC1N⊥平面AA1C1C,设AC1中点为D,连结DM,DN,可证BM∥DN,由BM⊥平面ACC1A1,可证DN⊥平面ACC1A1,即可证明平面AC1N⊥平面ACC1A1.
解答 (本小题共14分)
解:(Ⅰ)连结AB1交A1B于O,连结OM.
在△B1AC中,因为M,O分别为AC,AB1中点,
所以OM∥B1C. 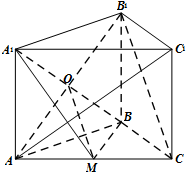
又因为OM?平面A1BM,B1C?平面A1BM,
所以B1C∥平面A1BM. …(4分)
(Ⅱ)因为侧棱AA1⊥底面ABC,BM?平面ABC,
所以AA1⊥BM.
又因为M为棱AC中点,AB=BC,所以BM⊥AC.
因为AA1∩AC=A,所以BM⊥平面ACC1A1.
所以BM⊥AC1.
因为M为棱AC中点,AC=2,所以AM=1.
又因为$A{A_1}=\sqrt{2}$,所以在Rt△ACC1和Rt△A1AM中,$tan∠A{C_1}C=tan∠{A_1}MA=\sqrt{2}$.
所以∠AC1C=∠A1MA,即∠AC1C+∠C1AC=∠A1MA+∠C1AC=90°.
所以A1M⊥AC1.
因为BM∩A1M=M,
所以AC1⊥平面A1BM. …(10分)
(Ⅲ)当点N为BB1中点时,即$\frac{BN}{{B{B_1}}}=\frac{1}{2}$,平面AC1N⊥平面AA1C1C.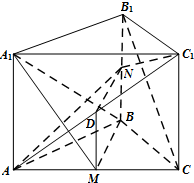
设AC1中点为D,连结DM,DN.
因为D,M分别为AC1,AC中点,
所以DM∥CC1,且$DM=\frac{1}{2}C{C_1}$.
又因为N为BB1中点,
所以DM∥BN,且DM=BN.
所以BM∥DN,
因为BM⊥平面ACC1A1,
所以DN⊥平面ACC1A1.
又因为DN?平面AC1N,所以平面AC1N⊥平面ACC1A1. …(14分)
点评 本题主要考查了平面与平面垂直的判定,直线与平面平行的判定,直线与平面垂直的判定,考查了空间想象能力和转化思想,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | {-1,0,2} | B. | {-1,0,1,2} | C. | {-1,0,2,3} | D. | {0,1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9x-16y+7=0 | B. | 16x+9y-25=0 | C. | 9x+16y-25=0 | D. | 16x-9y-7=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 不存在 | B. | 恰有一条 | C. | 恰有两条 | D. | 有无数条 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com