Question

10．已知二次函数y=$\frac{{x}^{2}}{4}$和直线y=kx+1交于A、B两点，∠AOB=120°，则S_△AOB=（　　）

• A． $\frac{3\sqrt{3}}{2}$
• B． 2
• C． $\frac{\sqrt{3}}{2}$
• D． $\frac{3}{4}$

Answer 1

分析 可设$A（{x}_{1}，\frac{{{x}_{1}}^{2}}{4}），B（{x}_{2}，\frac{{{x}_{2}}^{2}}{4}）$，联立直线方程和二次函数解析式消去y即可得到x²-4kx-4=0，所以根据韦达定理即可得到：x₁+x₂=4k，x₁x₂=-4．向量$\overrightarrow{OA}，\overrightarrow{OB}$的夹角为120°，所以根据向量夹角余弦的坐标公式，即可求出k，从而根据三角形的面积公式得到$S=\frac{1}{2}\sqrt{{{x}_{1}}^{2}+\frac{{{x}_{1}}^{4}}{16}}•\sqrt{{{x}_{2}}^{2}+\frac{{{x}_{2}}^{4}}{16}}sin120°$，带入x₁+x₂，x₁x₂的值即可求出S．

解答 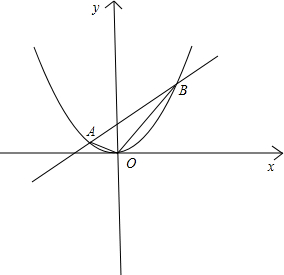解：如图，
设A（${x}_{1}，\frac{{{x}_{1}}^{2}}{4}$），B（${x}_{2}，\frac{{{x}_{2}}^{2}}{4}$）；
将y=kx+1代入y=$\frac{{x}^{2}}{4}$得：
x²-4kx-4=0；
∴x₁+x₂=4k，x₁x₂=-4；
根据已知条件，向量$\overrightarrow{OA}，\overrightarrow{OB}$的夹角为120°，$\overrightarrow{OA}=（{x}_{1}，\frac{{{x}_{1}}^{2}}{4}）$，$\overrightarrow{OB}=（{x}_{2}，\frac{{{x}_{2}}^{2}}{4}）$；
根据向量夹角的余弦的坐标公式，∴$-\frac{1}{2}=\frac{-4+1}{\sqrt{{{x}_{1}}^{2}+\frac{{{x}_{1}}^{4}}{16}}•\sqrt{{{x}_{2}}^{2}+\frac{{{x}_{2}}^{4}}{16}}}$；
∴$2\sqrt{1+\frac{1}{16}+\frac{（{x}_{1}+{x}_{2}）^{2}+8}{16}}=3$；
∴$2\sqrt{1+\frac{1}{16}+\frac{2{k}^{2}+1}{2}}=3$；
解得k=$±\frac{\sqrt{11}}{4}$；
${x}_{1}+{x}_{2}=±\sqrt{11}$；
∴S_△AOB=$\frac{1}{2}\sqrt{{{x}_{1}}^{2}+\frac{{{x}_{1}}^{4}}{16}}•\sqrt{{{x}_{2}}^{2}+\frac{{{x}_{2}}^{4}}{16}}sin120°$=$\frac{1}{2}\sqrt{（{x}_{1}{x}_{2}）^{2}[1+\frac{{{x}_{1}}^{2}+{{x}_{2}}^{2}}{16}+\frac{（{x}_{1}{x}_{2}）^{2}}{1{6}^{2}}]}$sin120°=$\frac{3\sqrt{3}}{2}$．
故选A．

点评 考查韦达定理，两向量夹角余弦的坐标公式，数量积的坐标运算，以及三角形的面积公式：S=$\frac{1}{2}absinC$．