
【题目】定义在![]() 上的函数
上的函数![]() ,如果满足:对任意
,如果满足:对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称函数
称函数![]() 的一个上界.已知函数
的一个上界.已知函数![]() ,
, ![]() .
.
(1)若函数![]() 为奇函数,求实数
为奇函数,求实数![]() 的值;
的值;
(2)在第(1)的条件下,求函数![]() 在区间
在区间![]() 上的所有上界构成的集合;
上的所有上界构成的集合;
(3)若函数![]() 在
在![]() 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)
;(3) ![]() .
.
【解析】试题分析:
(1)由函数为奇函数可得![]() ,即
,即![]() ,整理得
,整理得![]() ,可得
,可得![]() ,解得
,解得![]() ,经验证
,经验证![]() 不合题意.(2)根据单调性的定义可证明函数
不合题意.(2)根据单调性的定义可证明函数![]() 在区间
在区间![]() 上为增函数,从而可得
上为增函数,从而可得![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,故
,故![]() ,从而可得所有上界构成的集合为
,从而可得所有上界构成的集合为![]() .(3)将问题转化为
.(3)将问题转化为![]() 在
在![]() 上恒成立,整理得
上恒成立,整理得![]() 在
在![]() 上恒成立,通过判断函数的单调性求得
上恒成立,通过判断函数的单调性求得![]() 即可得到结果.
即可得到结果.
试题解析:
(1)∵函数![]() 是奇函数,
是奇函数,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得![]() ,
,
当![]() 时,
时, ![]() ,不合题意,舍去.
,不合题意,舍去.
∴![]() .
.
(2)由(1)得![]() ,
,
设![]() ,
,
令![]() ,且
,且![]() ,
,
∵![]()
![]() ;
;
∴![]() 在
在![]() 上是减函数,
上是减函数,
∴![]() 在
在![]() 上是单调递增函数,
上是单调递增函数,
∴![]() 在区间
在区间![]() 上是单调递增,
上是单调递增,
∴![]() ,即
,即![]() ,
,
∴![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,
,
∴![]() ,
,
故函数![]() 在区间
在区间![]() 上的所有上界构成的集合为
上的所有上界构成的集合为![]() .
.
(3)由题意知, ![]() 在
在![]() 上恒成立,
上恒成立,
∴![]() ,
,
∴![]() ,
,
因此![]() 在
在![]() 上恒成立,
上恒成立,
∴![]()
设![]() ,
, ![]() ,
, ![]() ,由
,由![]() 知
知![]() ,
,
设![]() ,则
,则
![]() ,
, ![]() ,
,
∴![]() 在
在![]() 上单调递减,
上单调递减, ![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() 在
在![]() 上的最大值为
上的最大值为![]() ,
, ![]() 在
在![]() 上的最小值为
上的最小值为![]() ,
,
∴![]() .
.
∴![]() 的取值范围
的取值范围![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知{an}是公差不为零的等差数列,a1=1,且a1 , a3 , a9成等比数列.
(1)求数列{an}的通项;
(2)设数列{an}的前n项和为Sn , 令 ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市上年度电价为0.80元/千瓦时,年用电量为![]() 千瓦时.本年度计划将电价降到0.55元/千瓦时~0.7元/千瓦时之间,而居民用户期望电价为0.40元/千瓦时(该市电力成本价为0.30元/千瓦时),经测算,下调电价后,该城市新增用电量与实际电价和用户期望电价之差成反比,比例系数为
千瓦时.本年度计划将电价降到0.55元/千瓦时~0.7元/千瓦时之间,而居民用户期望电价为0.40元/千瓦时(该市电力成本价为0.30元/千瓦时),经测算,下调电价后,该城市新增用电量与实际电价和用户期望电价之差成反比,比例系数为![]() .试问当地电价最低为多少元/千瓦时,可保证电力部门的收益比上年度至少增加20%.
.试问当地电价最低为多少元/千瓦时,可保证电力部门的收益比上年度至少增加20%.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知线段AB的端点A的坐标为![]() ,端点B是圆
,端点B是圆![]() :
:![]() 上的动点.
上的动点.
(1)求过A点且与圆![]() 相交时的弦长为
相交时的弦长为![]() 的直线
的直线![]() 的方程。
的方程。
(2)求线段AB中点M的轨迹方程,并说明它是什么图形。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和记为Sn , a1=2,an+1=Sn+2(n∈N*).
(Ⅰ)求{an}的通项公式;
(Ⅱ)求数列{nan}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知y=f(x)(x∈R)是偶函数,当x≥0时,f(x)=x2﹣2x.
(1)求f(x)的解析式;
(2)若不等式f(x)≥mx在1≤x≤2时都成立,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者.从符合条件的500名志愿者中随机抽取100名志愿者,其年龄频率分布直方图如图所示,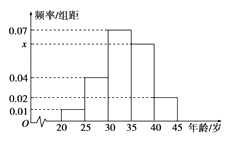
(1)求图中 ![]() 的值并根据频率分布直方图估计这500名志愿者中年龄在
的值并根据频率分布直方图估计这500名志愿者中年龄在 ![]() 岁的人数;
岁的人数;
(2)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取20名参加中心广场的宣传活动,再从这20名中采用简单随机抽样方法选取3名志愿者担任主要负责人.记这3名志愿者中“年龄低于35岁”的人数为 ![]() ,求
,求 ![]() 的分布列及均值.
的分布列及均值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com