
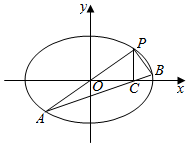
 如图,过坐标原点O的直线椭圆Г:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)于P,A两点,其中P在第一象限,B在椭圆Г上,直线AB与x轴交于点C.
如图,过坐标原点O的直线椭圆Г:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)于P,A两点,其中P在第一象限,B在椭圆Г上,直线AB与x轴交于点C.分析 (1)由题意可得c=$\sqrt{2}$,即a2-b2=2,将P($\sqrt{2}$,1)代入椭圆方程,解方程组可得a,b,进而得到椭圆方程;
(2)设A(x1,y1),P(-x1,-y1),B(x2,y2),代入椭圆方程,运用直线的斜率公式,化简即可得证;
(3)由两直线垂直的条件可得kBP•kAP=-1,由(2)的结论,运用直线的斜率公式,化简整理,再由a,b,c的关系和离心率公式,即可得到离心率.
解答 解:(1)由题意可得2c=2$\sqrt{2}$,即为c=$\sqrt{2}$,
即a2-b2=2,
将P($\sqrt{2}$,1)代入椭圆方程可得,$\frac{2}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=1,
解得a=2,b=$\sqrt{2}$,
则椭圆Г的标准方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1;
(2)证明:设A(x1,y1),P(-x1,-y1),B(x2,y2),
即有$\frac{{{x}_{1}}^{2}}{{a}^{2}}$+$\frac{{{y}_{1}}^{2}}{{b}^{2}}$=1,$\frac{{{x}_{2}}^{2}}{{a}^{2}}$+$\frac{{{y}_{2}}^{2}}{{b}^{2}}$=1,
两式相减可得,$\frac{{{x}_{1}}^{2}-{{x}_{2}}^{2}}{{a}^{2}}$+$\frac{{{y}_{1}}^{2}-{{y}_{2}}^{2}}{{b}^{2}}$=0,
则kBP•kBA=$\frac{{y}_{1}+{y}_{2}}{{x}_{1}+{x}_{2}}$•$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=$\frac{{{y}_{1}}^{2}-{{y}_{2}}^{2}}{{{x}_{1}}^{2}-{{x}_{2}}^{2}}$=-$\frac{{b}^{2}}{{a}^{2}}$;
(3)由BP⊥AP,可得kBP•kAP=-1,
由kBP•kBA=-$\frac{{b}^{2}}{{a}^{2}}$,可得kAP=$\frac{{a}^{2}}{{b}^{2}}$kBA,(*)
设P(x0,y0),则A(-x0,-y0),C(x0,0),
则kAP=$\frac{{y}_{0}}{{x}_{0}}$,kBA=kCA=$\frac{{y}_{0}}{2{x}_{0}}$,
代入(*),可得$\frac{{y}_{0}}{{x}_{0}}$=$\frac{{a}^{2}}{{b}^{2}}$•$\frac{{y}_{0}}{2{x}_{0}}$,
即有a2=2b2,由a2-b2=c2,
可得a2=2c2,e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$.
点评 本题考查椭圆的方程的求法,注意运用椭圆的性质和点满足椭圆方程,考查直线的斜率公式和点差法的运用,考查椭圆的离心率的求法,注意运用直线的斜率公式和离心率公式,属于中档题.


科目:高中数学 来源: 题型:填空题
| 次品数 | 0 | 1 | 2 | 3 | 5 |
| 频率 | 0.5 | 0.2 | 0.05 | 0.2 | 0.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,圆x2+y2=8内有一点P(-1,2),AB为过点P的弦.
如图,圆x2+y2=8内有一点P(-1,2),AB为过点P的弦.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com