
(本题满分12分)已知函数y=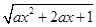 的定义域为R,解关于x的不等式
的定义域为R,解关于x的不等式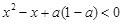
当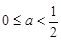 时,
时, ;当
;当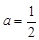 时,Ф;当
时,Ф;当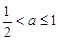 时,
时,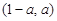 .
.
解析试题分析:由条件可得0≤a≤1,原不等式可化为(x-a)[x-(1-a)]>0,分0≤a< 、a=
、a= 、
、 <a≤1三种情况,分别求出不等式的解集.
<a≤1三种情况,分别求出不等式的解集.
解:∵函数y=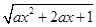 的定义域为R,∴
的定义域为R,∴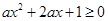 恒成立. …1分
恒成立. …1分
当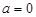 时,
时,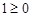 ,不等式恒成立;当
,不等式恒成立;当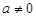 时,则
时,则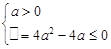
解得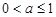 .综上,
.综上,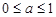 ………………………4分
………………………4分
由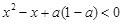 得
得 .……6分
.……6分
∵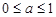 ,
,
∴(1)当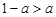 ,即
,即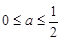 时,
时,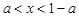 ;
;
(2)当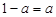 ,即
,即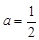 时,
时, ,不等式无解;
,不等式无解;
(3)当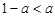 ,即
,即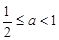 时,
时,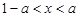 .………………………………10分
.………………………………10分
∴原不等式的解集为:当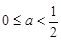 时,
时, ;当
;当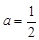 时,Ф;当
时,Ф;当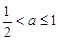 时,
时,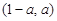 . ……………………12分
. ……………………12分
考点:本试题主要考查了二元一次不等式的解法,函数的恒成立问题,体现了分类讨论的数学思想,属于中档题.
点评:解决该试题的关键是由条件可得0≤a≤1,对于参数a,分0≤a< 、a=
、a= 、
、 <a≤1三种情况,分别求出不等式的解集.
<a≤1三种情况,分别求出不等式的解集.


科目:高中数学 来源: 题型:解答题
已知平面上的线段l及点P,在l上任取一点Q,线段PQ长度的最小值称为点P到线段l的距离,记作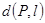 。
。
(1)已知点 ,线段
,线段 ,求
,求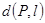 ;
;
(2)设A(-1,0),B(1,0),求点集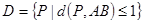 所表示图形的面积;
所表示图形的面积;
(3)若M(0,1),O(0,0),N(2,0),画出集合 所表示的图形。(本题满分14分)
所表示的图形。(本题满分14分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com