Question

18．若正方体ABCD-A₁B₁C₁D₁中，化简下列各式的结果为$\overrightarrow{A{C}_{1}}$的是（　　）

• A． $\overrightarrow{A{A}_{1}}$+$\overrightarrow{{A}_{1}{B}_{1}}$+$\overrightarrow{{B}_{1}D}$
• B． $\overrightarrow{AB}$+$\overrightarrow{{B}_{1}{C}_{1}}$+$\overrightarrow{D{D}_{1}}$
• C． $\overrightarrow{AB}$+$\overrightarrow{B{B}_{1}}$+$\overrightarrow{{B}_{1}{D}_{1}}$
• D． $\overrightarrow{A{B}_{1}}$+$\overrightarrow{C{C}_{1}}$

Answer 1

分析 可先画出正方体，根据图形及相等向量、向量加法的集合意义即可化简每个选项，从而得出正确答案．

解答 解：如图，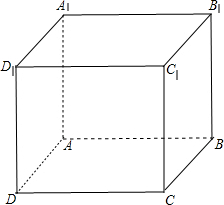
A.$\overrightarrow{A{A}_{1}}+\overrightarrow{{A}_{1}{B}_{1}}+\overrightarrow{{B}_{1}D}=\overrightarrow{AD}$；
B.$\overrightarrow{AB}+\overrightarrow{{B}_{1}{C}_{1}}+\overrightarrow{D{D}_{1}}$=$\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{C{C}_{1}}=\overrightarrow{A{C}_{1}}$；
C.$\overrightarrow{AB}+\overrightarrow{B{B}_{1}}+\overrightarrow{{B}_{1}{D}_{1}}=\overrightarrow{A{D}_{1}}$；
D.$\overrightarrow{A{B}_{1}}+\overrightarrow{C{C}_{1}}=\overrightarrow{A{B}_{1}}+\overrightarrow{B{B}_{1}}$，由图形看出显然$\overrightarrow{A{B}_{1}}+\overrightarrow{B{B}_{1}}≠\overrightarrow{A{C}_{1}}$；
∴B正确．
故选B．

点评 考查相等向量的概念，以及向量加法的几何意义．