
分析 根据实系数一元二次方程有虚根的条件:判别式小于0,以及共轭复数的积与模的关系,根据二次不等式的解法,以及p、q均为真命题,求交集即可得到所求范围.
解答 解:命题p:实系数一元二次方程x2+mx+2=0有虚根,
等价为m2-8<0,解得-2$\sqrt{2}$<m<2$\sqrt{2}$①
命题q:关于x的方程:2x2-4(m-1)x+m2+7=0(m∈R)的两个虚根的模的和不大于$4\sqrt{2}$,
等价为16(m-1)2-8(m2+7)<0,解得-1<m<5,②
设两个虚根为x1,x2,
则有x1+x2=2(m-1),x1x2=$\frac{1}{2}$(m2+7),
由x1,x2,互为共轭复数,可得|x1|+|x2|=2|x1|=2$\sqrt{{x}_{1}{x}_{2}}$=$\sqrt{2({m}^{2}+7)}$,
即有$\sqrt{2({m}^{2}+7)}$≤4$\sqrt{2}$,解得-3≤m≤3,③
若p、q均为真命题,
由①②③可得,-1<m<2$\sqrt{2}$.
可得实数m的取值范围为(-1,2$\sqrt{2}$).
点评 本题考查实系数一元二次方程有虚根的条件,以及复数的模的定义,考查二次不等式的解法,以及命题的真假判断,考查运算能力,属于中档题.


 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{6}$ | B. | $-\frac{7}{6}$ | C. | 4 | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
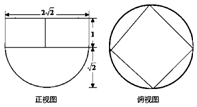
| A. | $2+\frac{{4\sqrt{2}π}}{3}$ | B. | $4+\frac{{8\sqrt{2}π}}{3}$ | C. | $2+\frac{{8\sqrt{2}π}}{3}$ | D. | $4+\frac{{4\sqrt{2}π}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 以直角三角形的一直角边为轴旋转所得的旋转体是圆锥 | |
| B. | 以直角梯形的一腰为轴旋转所得的旋转体是圆台 | |
| C. | 有一个面是多边形,其余各面都是三角形的几何体叫做棱锥 | |
| D. | 圆锥的侧面展开图为扇形,这个扇形的半径为圆锥底面圆的半径 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| a | b | c | d | |
| r | 0.80 | 0.76 | 0.67 | 0.82 |
| m | 100 | 113 | 121 | 99 |
| A. | a | B. | b | C. | c | D. | d |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com