Question

15．一次测试中，为了了解学生的学习情况，从中抽取了n个学生的成绩（满分为100分）进行统计．按照[50，60），[60，70），[70，80），[80，90），[90，100]的分组作出频率分布直方图，并作出样本分数的茎叶图（图中仅列出得分在[50，60），[90，100]的数据）．
（1）求样本容量n和频率分布直方图中x，y的值；
（2）在选取的样本中，从成绩是80分以上（含80分）的同学中随机抽取2名参加志愿者活动，所抽取的2名同学中得分都在[80，90）内的概率．

Answer 1

分析 （1）根据频率分布直方图的性质求得样本容量n和频率分布直方图中x、y的值．
（2）由题意可知，分数在[80，90）内的有4人，设为A，B，C，D；分数在[90，100]内的有2人，设为a，b，用列举法求得所有的抽法有15种，而满足条件的抽法有6种，由此求得所求事件的概率．

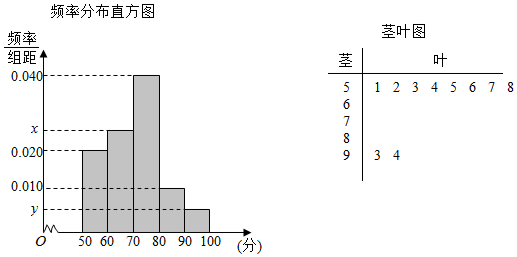
解答 解：（1）由题意可知，样本容量$n=\frac{8}{0.02×10}=40$，$y=\frac{2}{40}÷10=0.005$，$x=\frac{1-（0.02+0.04+0.01+0.005）×10}{10}=0.025$．
（2）由题意，分数在[80，90）内的有4人，设为A，B，C，D；分数在[90，100]内的有2人，设为a，b；
从成绩是8（0分）以上（含80分）的6名同学中随机抽取2名同学的所有可能的结果为：{A，B}，{A，C}，{A，D}，{A，a}，{A，b}，{B，C}，{B，D}，{B，a}，{B，b}，{C，D}，{C，a}，{C，b}，{D，a}，{D，b}，{a，b}，共15个
根据题意，这些基本事件的出现是等可能的．事件所包含的基本事件有：{A，B}，{A，C}，{A，D}，{B，C}，{B，D}，{C，D}，共6个．
∴P=$\frac{6}{15}$=0.4．

点评 本题主要考查等可能事件的概率，频率分布直方图的应用，属于中档题．