练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．平行直线l1：3x+4y-12=0与l2：6x+8y-15=0之间的距离为（　　）
    A．$\frac{3}{10}$B．$\frac{9}{10}$C．$\frac{3}{5}$D．$\frac{9}{5}$

    分析 直接利用平行线之间的距离公式求解即可．

    解答 解：平行直线l1：3x+4y-12=0与l2：6x+8y-15=0之间的距离为：$\frac{|-15+24|}{\sqrt{{6}^{2}+{8}^{2}}}$=$\frac{9}{10}$．
    故选：B．

    点评 本题考查平行线之间的距离的求法，考查计算能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    14．某校高三期中考试后，数学教师对本次全部数学成绩按 1：20进行分层抽样，随机抽取了 20名学生的成绩为样本，成绩用茎叶图记录如图所示，但部分数据不小心丢失，同时得到如下表所示的频率分布表：
    分数段（分）[50，70）[70，90）[90，110）[110，130）[130，150]总计
    频数b
    频率a0.25
    （Ⅰ）求表中 a，b 的值及成绩在[90，110）范围内的个体数，并估计这次考试全校高三数学成绩的及格率（成绩在[90，150]内为及格）；
    （Ⅱ）设茎叶图中成绩在[100，120）范围内的样本的中位数为m，若从成绩在[100，120）范围内的样品中每次随机抽取1个，每次取出不放回，连续取两次，求取出两个样本中恰好一个是数字m的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．已知数列{an}满足a1=1，an+1=$\frac{n+1}{n}$an+2n+2，则a8=120．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．函数y=f（x）是实数集R上的偶函数，且在（-∞，0]上是单调递增函数，若f（a）≤f（2），则实数a的取值范围是（　　）
    A．a≥-2B．a≥2或a≤-2C．-2≤a≤2D．a≤2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知数列{an}中，a1=1，an+an+1=3n+1（n∈N*）
    （1）求数列{a2n}和数列{a2n-1}的通项公式；
    （2）求数列{an}的前2n项和S2n．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．在△ABC中，角A，B，C所对的边为a，b，c，且b，a，b+c成等比数列．
    （1）证明：cosA=$\frac{c-b}{2b}$；
    （2）求$\frac{a+c}{b}$的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

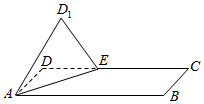    16．在长方形ABCD中，AD=2，AB=4，点E是边CD上的一动点，将△ADE沿直线AE翻折到△AD1E，使得二面角D1-AE-B为直二面角，则cos∠D1AB的最大值为（　　）
    A．$\frac{1}{4}$B．$\frac{1}{2}$C．$\frac{\sqrt{2}}{2}$D．$\frac{\sqrt{3}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．在△ABC中，a=4，b=5，c=6，则$\frac{sinC}{sin2A}$=（　　）
    A．$\frac{3}{4}$B．$\frac{4}{5}$C．1D．$\frac{4}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知命题p：x＞k，q：$\frac{3}{x+1}$≥1，若p是q的必要不充分条件，则实数k的取值范围是（　　）
    A．（2，+∞）B．[2，+∞）C．（-∞，-1）D．（-∞，-1]

    查看答案和解析>>

    同步练习册答案