
分析 由已知得:4(sin2x)2=1+2sinθcosθ,将cos2x=sinθcosθ代入得:4(sin2x)2=1+2cos2x,整理可得4cos22x+cos2x-2=0,即可得解.
解答 解:2sin2x=sinθ+cosθ,
平方得:4(sin2x)2=1+2sinθcosθ,
将cos2x=sinθcosθ代入得:
4(sin2x)2=1+2cos2x,
4(1-cos22x)=1+2cos2x,
4(1-cos22x)=1+(1+cos2x),
4cos22x+cos2x-2=0,
cos2x=$\frac{-1±\sqrt{33}}{8}$.
又cos2x=2cos2x-1=2sinxcosx-1=-(sinx-cosx)2<0,
可得:cos2x=$\frac{-1-\sqrt{33}}{8}$.
故答案为:$\frac{-1-\sqrt{33}}{8}$.
点评 本题主要考查了三角函数恒等变换的应用,一元二次方程的解法,属于基本知识的考查.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:高中数学 来源: 题型:填空题
 如图:平面上两点P(0,1),Q(3,6),在直线y=x上取两点M,N,使$|MN|=\sqrt{2}$且使|PM|+|MN|+|NQ|的值取最小,则N的坐标为$(\frac{9}{4},\frac{9}{4})$.
如图:平面上两点P(0,1),Q(3,6),在直线y=x上取两点M,N,使$|MN|=\sqrt{2}$且使|PM|+|MN|+|NQ|的值取最小,则N的坐标为$(\frac{9}{4},\frac{9}{4})$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
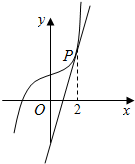 如图,已知函数f(x)=ax3+b,其图象上一点P处的切线为 l:y=4x-4,且点P的横坐标为2.
如图,已知函数f(x)=ax3+b,其图象上一点P处的切线为 l:y=4x-4,且点P的横坐标为2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com