
【题目】连续投掷两次骰子得到的点数分别为m,n,向量 ![]() 与向量
与向量 ![]() 的夹角记为α,则α
的夹角记为α,则α ![]() 的概率为( )
的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:根据题意,m、n的情况各有6种,则 ![]() 的情况有6×6=36种, 又由题意,向量
的情况有6×6=36种, 又由题意,向量 ![]() ,向量
,向量 ![]() ,
,
则cosα= ![]() ,
,
若α ![]() ,则
,则 ![]() <
< ![]() <1,
<1,
化简可得m2>n2 , 即m>n,
则 ![]() 的坐标可以为:(2,1),(3,1),(3,2),(4,1),(4,2),(4,3),(5,1),(5,2),(5,3),(5,4),(6,1),(6,2),(6,3),(6,4),(6,5),共有15种情况;
的坐标可以为:(2,1),(3,1),(3,2),(4,1),(4,2),(4,3),(5,1),(5,2),(5,3),(5,4),(6,1),(6,2),(6,3),(6,4),(6,5),共有15种情况;
则α ![]() 的概率为
的概率为 ![]() =
= ![]() ,
,
故选B.
根据题意,由分步计数原理分析可得向量 ![]() 的情况数目;进而根据向量的数量积公式可得cosα=
的情况数目;进而根据向量的数量积公式可得cosα= ![]() ,由余弦函数的性质可得若α
,由余弦函数的性质可得若α ![]() ,则
,则 ![]() <
< ![]() <1,对其变形化简可得m>n,由列举法可得其情况数目,由等可能事件的概率公式计算可得答案.
<1,对其变形化简可得m>n,由列举法可得其情况数目,由等可能事件的概率公式计算可得答案.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,A,B,C的坐标分别为(﹣ ![]() ,0),(
,0),( ![]() ,0),(m,n),G,O′,H分别为△ABC的重心,外心,垂心.
,0),(m,n),G,O′,H分别为△ABC的重心,外心,垂心. 
(1)写出重心G的坐标;
(2)求外心O′,垂心H的坐标;
(3)求证:G,H,O′三点共线,且满足|GH|=2|OG′|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们把形如 ![]() 的函数称为幂指函数,幂指函数在求导时,可以利用对法数:在函数解析式两边求对数得
的函数称为幂指函数,幂指函数在求导时,可以利用对法数:在函数解析式两边求对数得 ![]() ,两边对x求导数,得
,两边对x求导数,得 ![]() ,于是
,于是 ![]() ,运用此方法可以求得函数
,运用此方法可以求得函数 ![]() 在(1,1)处的切线方程是 .
在(1,1)处的切线方程是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ax2﹣(2a+1)x+2lnx(a∈R). (Ⅰ)若曲线y=f(x)在x=1和x=3处的切线互相平行,求a的值;
ax2﹣(2a+1)x+2lnx(a∈R). (Ⅰ)若曲线y=f(x)在x=1和x=3处的切线互相平行,求a的值;
(Ⅱ)求f(x)的单调区间;
(Ⅲ)设g(x)=x2﹣2x,若对任意x1∈(0,2],均存在x2∈(0,2],使得f(x1)<g(x2),求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知矩形ABCD中,AB=2,AD=1,M为CD的中点.如图将△ADM沿AM折起,使得平面ADM⊥平面ABCM.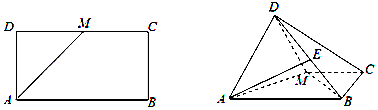
(Ⅰ)求证:BM⊥平面ADM;
(Ⅱ)若点E是线段DB上的中点,求三棱锥E﹣ABM的体积V1与四棱锥D﹣ABCM的体积V2之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥P﹣ABCD中,底面ABCD是矩形,PA⊥平面ABCD,M、N分别是AB、PC的中点,PA=AD=1,AB=2. 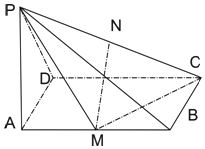
(1)求证:MN∥平面PAD;
(2)求证:平面PMC⊥平面PCD;
(3)求点D到平面PMC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的部分图象如图所示,则关于f(x)的说法正确的是( )
)的部分图象如图所示,则关于f(x)的说法正确的是( ) 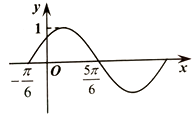
A.对称轴方程是x= ![]() +2kπ(k∈Z)
+2kπ(k∈Z)
B.φ=﹣ ![]()
C.最小正周期为π
D.在区间( ![]() ,
, ![]() )上单调递减
)上单调递减
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=3x , g(x)=|x+a|﹣3,其中a∈R. (Ⅰ)若函数h(x)=f[g(x)]的图象关于直线x=2对称,求a的值;
(Ⅱ)给出函数y=g[f(x)]的零点个数,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com