
分析 根据有理数指数幂的运算性质,对数的运算性质,逐一代入运算可得答案.
解答 解:(1)(2$\frac{1}{4}$)${\;}^{\frac{1}{2}}$-(-9.6)0-(3$\frac{3}{8}$)${\;}^{-\frac{2}{3}}$+0.1-2=($\frac{9}{4}$)${\;}^{\frac{1}{2}}$-(-9.6)0-($\frac{27}{8}$)${\;}^{-\frac{2}{3}}$+($\frac{1}{10}$)-2=$\frac{3}{2}$-1-$\frac{4}{9}$+100=100$\frac{1}{18}$;
(2)$\frac{lo{g}_{m}(2a)-lo{g}_{m}(2b)}{lo{g}_{m}a-lo{g}_{m}b}$=$\frac{{log}_{m}^{\;}(\frac{2a}{2b})}{{log}_{m}^{\;}(\frac{a}{b})}$=$\frac{{log}_{m}^{\;}(\frac{a}{b})}{{log}_{m}^{\;}(\frac{a}{b})}$=1(a,b>0,a≠b);
(3)(eln3+e${\;}^{\frac{1}{2}ln4}$)(eln3-e${\;}^{\frac{1}{2}}$ln4)=(3+2)(3-2)=5;
(4)$\frac{lo{g}_{27}16}{lo{g}_{3}8}$=$\frac{\frac{4}{3}{log}_{3}2}{3{log}_{3}2}$=$\frac{4}{9}$
点评 本题考查的知识点是有理数指数幂的运算性质,对数的运算性质,熟练掌握有理数指数幂的运算性质,对数的运算性质,是解答的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
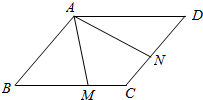 如图,已知菱形ABCD的边长为2,∠BAD=120°,M,N分别为BC、CD上的点,$\overrightarrow{BM}$=λ$\overrightarrow{BC}$,$\overrightarrow{DN}$=μ$\overrightarrow{DC}$,λ,μ∈(0,1),记$\overrightarrow{AM}$=$\overrightarrow{a}$,$\overrightarrow{AN}$=$\overrightarrow{b}$.
如图,已知菱形ABCD的边长为2,∠BAD=120°,M,N分别为BC、CD上的点,$\overrightarrow{BM}$=λ$\overrightarrow{BC}$,$\overrightarrow{DN}$=μ$\overrightarrow{DC}$,λ,μ∈(0,1),记$\overrightarrow{AM}$=$\overrightarrow{a}$,$\overrightarrow{AN}$=$\overrightarrow{b}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
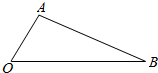 如图所示,在△AOB中,已知∠AOB=60°,OA=2,OB=5,在线段OB上任取一点C,则△AOC为钝角三角形的概率为$\frac{2}{5}$.
如图所示,在△AOB中,已知∠AOB=60°,OA=2,OB=5,在线段OB上任取一点C,则△AOC为钝角三角形的概率为$\frac{2}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com