
分析 ${∫}_{-2}^{2}$($\sqrt{4-x^2}$+sinx)dx=${∫}_{-2}^{2}$$\sqrt{4-x^2}$dx+${∫}_{-2}^{2}$sinxdx,由定积分的几何意义和求解方法可得.
解答 解:${∫}_{-2}^{2}$($\sqrt{4-x^2}$+sinx)dx=${∫}_{-2}^{2}$$\sqrt{4-x^2}$dx+${∫}_{-2}^{2}$sinxdx,
∵${∫}_{-2}^{2}$$\sqrt{4-x^2}$dx表示圆x2+y2=4与x轴围成的半圆的面积,
∴${∫}_{-2}^{2}$$\sqrt{4-x^2}$dx=$\frac{1}{2}$×π×22=2π,
又${∫}_{-2}^{2}$sinxdx=-cosx${|}_{-2}^{2}$=0,
∴${∫}_{-2}^{2}$($\sqrt{4-x^2}$+sinx)dx=2π,
故答案为:2π.
点评 本题考查定积分的求解,涉及定积分的几何意义,属中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $sin\frac{b-m}{a-m}<sin\frac{b+m}{a+m}<sin\frac{b}{a}$ | B. | $sin\frac{b-m}{a-m}>sin\frac{b+m}{a+m}>sin\frac{b}{a}$ | ||
| C. | $sin\frac{b-m}{a-m}>sin\frac{b}{a}>sin\frac{b+m}{a+m}$ | D. | $sin\frac{b-m}{a-m}<sin\frac{b}{a}<sin\frac{b+m}{a+m}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
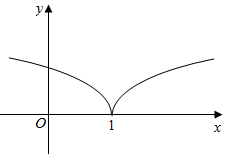 如果函数y=f(x)的定义域为R,并且大致图象如图所示,那么函数的解析式可以是f(x)=$\left\{\begin{array}{l}{lnx,x≥1}\\{ln(2-x),x<1}\end{array}\right.$(只需写出一个正确答案)
如果函数y=f(x)的定义域为R,并且大致图象如图所示,那么函数的解析式可以是f(x)=$\left\{\begin{array}{l}{lnx,x≥1}\\{ln(2-x),x<1}\end{array}\right.$(只需写出一个正确答案)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com