
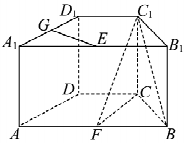
 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E、F、G分别是棱A1B1、AB、A1D1的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E、F、G分别是棱A1B1、AB、A1D1的中点.分析 取AF的中点M,连接DM,得DM⊥CD.以DM,DC,DD1所在直线分别为x,y,z轴建立空间直角坐标系,利用向量法求解.
解答 解:因为AB=4,BC=CD=2,F是棱AB的中点,
所以BF=BC=CF,△BCF为正三角形,因为ABCD为等腰梯形,
所以∠BAD=∠ABC=60°,取AF的中点M,
连接DM,则DM⊥AB,所以DM⊥CD.
以DM,DC,DD1所在直线分别为x,y,z轴建立空间直角坐标系,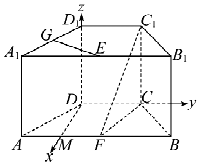
则D(0,0,0),$A(\sqrt{3},-1,0)$,$F(\sqrt{3},1,0)$C(0,2,0),C1(0,2,2),$E(\sqrt{3},1,2)$,$G(\frac{{\sqrt{3}}}{2},-\frac{1}{2},2)$,$B(\sqrt{3},3,0)$,
所以$\overrightarrow{CF}=(\sqrt{3},-1,0)$,$\overrightarrow{C{C_1}}=(0,0,2)$,$\overrightarrow{F{C_1}}=(-\sqrt{3},1,2)$.
设平面CC1F的法向量为$\overrightarrow n=(x,y,z)$,则$\left\{\begin{array}{l}\overrightarrow n•\overrightarrow{CF}=0\\ \overrightarrow n•\overrightarrow{C{C_1}}=0\end{array}\right.$
∴$\left\{\begin{array}{l}\sqrt{3}x-y=0\\ z=0\end{array}\right.$取$\overrightarrow n=(1,\sqrt{3},0)$.
(Ⅰ)证明:GE的方向向量为$(\frac{{\sqrt{3}}}{2},\frac{3}{2},0)$,
∵$\overrightarrow{GE}∥\overrightarrow n$,∴GE⊥平面FCC1.
(Ⅱ)解:$\overrightarrow{FB}=(0,2,0)$,设平面BFC1的法向量为$\overrightarrow{n_1}=({x_1},{y_1},{z_1})$,则$\left\{\begin{array}{l}\overrightarrow{n_1}•\overrightarrow{FB}=0\\ \overrightarrow{n_1}•\overrightarrow{F{C_1}}=0\end{array}\right.$
所以$\left\{\begin{array}{l}{y_1}=0\\-\sqrt{3}{x_1}+{y_1}+2{z_1}=0\end{array}\right.$取$\overrightarrow{n_1}=(2,0,\sqrt{3})$,
则$\overrightarrow n•\overrightarrow{n_1}=2×1-\sqrt{3}×0+0×\sqrt{3}=2$,$|\overrightarrow n|=\sqrt{1+{{(\sqrt{3})}^2}}=2$,$|\overrightarrow{n_1}|=\sqrt{{2^2}+0+{{(\sqrt{3})}^2}}=\sqrt{7}$,
所以$cos<\overrightarrow n,\overrightarrow{n_1}>=\frac{{\overrightarrow n•\overrightarrow{n_1}}}{{|\overrightarrow n|•|\overrightarrow{n_1}|}}=\frac{2}{{2×\sqrt{7}}}=\frac{{\sqrt{7}}}{7}$,由图可知二面角B-FC1-C为锐角,
所以二面角B-FC1-C的余弦值为$\frac{{\sqrt{7}}}{7}$.
点评 本题考查了空间线面垂直的判定,向量法求二面角,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $y=±\frac{3}{4}x$ | B. | $y=±\frac{4}{3}x$ | C. | $y=±\frac{16}{9}x$ | D. | $y=±\frac{9}{16}x$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
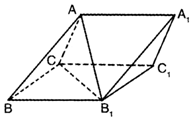 如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,AC=AB1.
如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,AC=AB1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| A组 | B组 | 合计 | |
| 男性 | 26 | 24 | 50 |
| 女性 | 30 | 20 | 50 |
| 合计 | 56 | 44 | 100 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| k0 | 0.455 | 0.708 | 1.323 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其导函数的图象f'(x)如图所示,则$f({\frac{π}{2}})$的值为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其导函数的图象f'(x)如图所示,则$f({\frac{π}{2}})$的值为( )| A. | $2\sqrt{3}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{32}$ | B. | $\frac{9}{32}$ | C. | $\frac{9}{16}$ | D. | $\frac{5}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com