
分析 由定积分的几何意义和椭圆的知识可得.
解答 解:由y=$\sqrt{5-\frac{5}{9}{x}^{2}}$平方整理可得$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1,
∴${∫}_{0}^{3}$$\sqrt{5-\frac{5}{9}{x}^{2}}$dx表示椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的四分之一个椭圆的面积,
同理可得${∫}_{0}^{3}$$\sqrt{3-\frac{1}{3}{x}^{2}}$dx表示椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{3}$=1的四分之一个椭圆的面积,
故${∫}_{0}^{3}$$\sqrt{5-\frac{5}{9}{x}^{2}}$dx>${∫}_{0}^{3}$$\sqrt{3-\frac{1}{3}{x}^{2}}$dx
点评 本题考查定积分的几何意义,涉及椭圆的知识,属基础题.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AB=4,BC=$\frac{3}{2}$,CD=$\frac{5}{2}$,∠A=$\frac{π}{3}$,cos∠ADB=$\frac{1}{7}$.
如图,在四边形ABCD中,AB=4,BC=$\frac{3}{2}$,CD=$\frac{5}{2}$,∠A=$\frac{π}{3}$,cos∠ADB=$\frac{1}{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
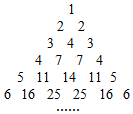 如图三角形数阵满足:
如图三角形数阵满足:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | l垂直于平面α内的一条直线 | B. | l垂直于平面α内的两条直线 | ||
| C. | l垂直于平面α内的无数条直线 | D. | l垂直于平面α内的任一条直线 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | cos$\frac{α}{4}$ | B. | -cos$\frac{α}{4}$ | C. | sin$\frac{α}{4}$ | D. | -sin$\frac{α}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)在区间[0,$\frac{π}{2}$]内是增函数 | |
| B. | 若?x1≠x2,f(x1)=f(x2)=0,则x1-x2必是π的整数倍 | |
| C. | f(x)的图象关于点(-$\frac{π}{12}$+$\frac{kπ}{2}$,0)(k∈Z)对称 | |
| D. | f(x)的图象关于直线x=$\frac{π}{12}$对称 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com