
分析 求出函数f(x)=|sin($\frac{π}{2}$x+$\frac{π}{4}$)|,(x<0)关于y轴对称的解析式,利用数形结合即可得到结论.
解答 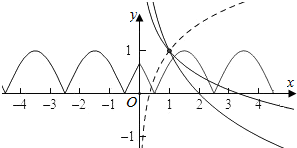 解:若x>0,则-x<0,此时f1(-x)=|sin(-$\frac{π}{2}$x+$\frac{π}{4}$)|=|sin($\frac{π}{2}$x-$\frac{π}{4}$)|,
解:若x>0,则-x<0,此时f1(-x)=|sin(-$\frac{π}{2}$x+$\frac{π}{4}$)|=|sin($\frac{π}{2}$x-$\frac{π}{4}$)|,
若函数关于y轴对称,则f1(-x)=|sin($\frac{π}{2}$x-$\frac{π}{4}$)|=f1(x),
即函数f(x)=|sin($\frac{π}{2}$x+$\frac{π}{4}$)|,x<0时关于y轴对称的函数为:
f1(x)=|sin($\frac{π}{2}$x-$\frac{π}{4}$)|,x>0,
作出函数f(x)的图象以及y=|sin($\frac{π}{2}$x-$\frac{π}{4}$)|的图象如图:
∵函数f(x)=logax+1恒过定点(1,1),
∴若a>1,则f(x)=logax+1与f1(x)=|sin($\frac{π}{2}$x-$\frac{π}{4}$)|,x>0,只有一个交点,不满足条件.
若0<a<1,由f1(x)=|sin($\frac{π}{2}$x-$\frac{π}{4}$)|=0得$\frac{π}{2}$x-$\frac{π}{4}$=kπ,即x=2k+$\frac{1}{2}$,
则k=1时,x=2+$\frac{1}{2}$=$\frac{5}{2}$,即第2个零点为$\frac{5}{2}$,
k=2时,x=4+$\frac{1}{2}$=$\frac{9}{2}$,即第3个零点为$\frac{9}{2}$,
若两个函数有3个交点,
则满足$\left\{\begin{array}{l}{f(\frac{5}{2})>0}\\{f(\frac{9}{2})<0}\end{array}\right.$,即$\left\{\begin{array}{l}{lo{g}_{a}\frac{5}{2}+1>0}\\{lo{g}_{a}\frac{9}{2}+1<0}\end{array}\right.$,
即$\left\{\begin{array}{l}{lo{g}_{a}\frac{5}{2}>-1}\\{lo{g}_{a}\frac{9}{2}<-1}\end{array}\right.$,即$\left\{\begin{array}{l}{\frac{5}{2}<\frac{1}{a}}\\{\frac{9}{2}>\frac{1}{a}}\end{array}\right.$,即$\left\{\begin{array}{l}{a<\frac{2}{5}}\\{a>\frac{2}{9}}\end{array}\right.$,即$\frac{2}{9}$<a<$\frac{2}{5}$,
故答案为:($\frac{2}{9}$,$\frac{2}{5}$)
点评 本题主要考查分段函数的应用,作出函数关于y对称的图象,利用数形结合的思想是解决本题的关键.综合性较强,有一定的难度.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | -$\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 物理 | 化学 | 生命科学 | 政治 | 历史 | 地理 | |
| 甲校 | 35 | 20 | 15 | 7 | 8 | 15 |
| 乙校 | 30 | 14 | 16 | 11 | 14 | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com