Question

10．如图，四棱锥P-ABCD中，底面ABCD为平行四边形，∠DAB=60°，AB=2AD=2，PD⊥底面ABCD，E为棱PC的中点．
（1）PA∥平面BDE；
（2）证明：PA⊥BD．

Answer 1

分析 （1）连结AC，BD，交于点O，连结OE，则OE∥AP，由此能证明PA∥平面BDE．
（2）因为∠DAB=60°，AB=2AD，由余弦定理得BD=$\sqrt{3}$AD，利用勾股定理证明BD⊥AD，根据PD⊥底面ABCD，易证BD⊥PD，根据线面垂直的判定定理和性质定理，可证PA⊥BD；

解答 解：（1）证明：连结AC，BD，交于点O，
∵四边形ABCD为平行四边形，∴O是AC中点，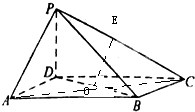
∵E是PC中点，∴OE∥AP，
又AP?平面BDE，OE?平面BDE，
∴PA∥平面BDE．
（2）证明：因为∠DAB=60°，AB=2AD，由余弦定理得BD=$\sqrt{3}$AD，
从而BD²+AD²=AB²，故BD⊥AD，
又PD⊥底面ABCD，可得BD⊥PD，
所以BD⊥平面PAD．故PA⊥BD．

点评 本题主要考查线面垂直的性质定理和判定定理，以及点到面的距离，考查了同学们观察、推理以及创造性地分析问题、解决问题能力，属于中档题．